Đề bài
Cho tam giác ABC. Trên tia đối của tia AB lấy điểm D sao cho \(AD = AC.\) Trên tia đối của tia AC lấy điểm E sao cho AE = AB. Chứng minh rằng BCDE là hình thang.
Phương pháp giải - Xem chi tiết
Tứ giác có hai cạnh đối song song là hình thang.
Lời giải chi tiết
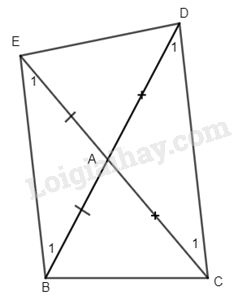
Ta có AD = AC (gt) \( \Rightarrow \Delta ACD\) cân tại A
\( \Rightarrow \widehat {{D_1}} = \widehat {{C_1}} =\dfrac {{{{180}^ \circ } - \widehat {DAC}}}{ 2}\)
Tương tự \(\Delta ABE\) cân tại A (do AE=AB)
\(\Rightarrow \widehat {{B_1}} = \widehat {{E_1}} =\dfrac {{{{180}^ \circ } - \widehat {BAE}} }{2}\)
Mà \(\widehat {DAC} = \widehat {BAE}\) (đối đỉnh) \( \Rightarrow \widehat {{B_1}} = \widehat {{D_1}}\) .
Mà \(\widehat {{B_1}}\) và \(\widehat {{D_1}}\) ở vị trí so le trong \( \Rightarrow BE// CD\)
Do đó BCDE là hình thang.
dapandethi.vn
