1. Các kiến thức cần nhớ
Để cộng (hay trừ) hai đa thức, ta làm như sau:
Bước 1: Viết hai đa thức trong dấu ngoặc
Bước 2: Thực hiện bỏ dấu ngoặc (theo quy tắc dấu ngoặc)
Bước 3: Nhóm các hạng tử đồng dạng
Bước 4: Cộng, trừ các đơn thức đồng dạng.
Ví dụ: Cho đa thức \(P(x) = 3 + 5{x^2} - 3{x^3} + 4{x^2} - 2x - {x^3} + 5{x^5}.\) Thu gọn và sắp xếp đa thức $P\left( x \right)$
Giải
\(P(x) = 3 + 5{x^2} - 3{x^3} + 4{x^2} - 2x - {x^3} + 5{x^5}\)
\( = 5{x^5} + \left( { - 3{x^3} - {x^3}} \right) + \left( {5{x^2} + 4{x^2}} \right) - 2x + 3\)
\( = 5{x^5} - 4{x^3} + 9{x^2} - 2x + 3\)
Ví dụ 2: Cho 2 đa thức
\(A = {x^2}-2y + xy + 1\)
\(B = {x^2} + y - {x^2}{y^2} - 1\)
Tìm đa thức C = A +B
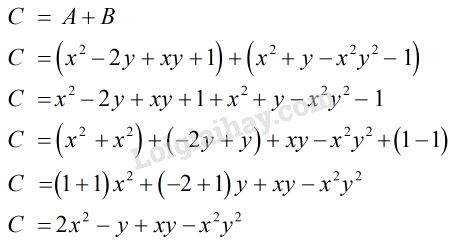
Vậy đa thức \(C = 2{x^2}-y + xy - {x^2}{y^2}\)
2. Các dạng toán thường gặp
Dạng 1: Tính tổng, hiệu hai đa thức
Phương pháp:
Thực hiện phép cộng (trừ) hai đa thức.
Dạng 2: Tìm một trong hai đa thức biết đa thức tổng hoặc đa thức hiệu và đa thức còn lại
Phương pháp:
+ Nếu \(M + B = A\) thì \(M = A - B.\)
+ Nếu \(M - B = A\) thì \(M = A + B.\)
+ Nếu \(A - M = B\) thì \(M = A - B.\)
Dạng 3: Tính giá trị của đa thức tại giá trị cho trước
Phương pháp:
Khi tính giá trị của đa thức tại các giá trị cho trước của các biến, ta thu gọn đa thức và chú ý nhận xét các đặc điểm của đa thức (nếu có) để thực hiện hợp lý các phép tính.
