Bài 1: (1đ) Thực hiện phép tính:
1) \(A = \sqrt {12} – 2\sqrt {48} + \dfrac{7}{5}\sqrt {75} \)
2) \(B = \sqrt {14 – 6\sqrt 5 } + \sqrt {{{\left( {2 – \sqrt 5 } \right)}^2}} \)
Bài 2: (2,5đ)
1)Cho biểu thức \(A = \dfrac{{\sqrt x + 4}}{{\sqrt x + 2}}\left( {x \ge 0} \right)\). Tính giá trị biểu thức \(A\) khi \(x = 36\).
2)Rút gọn biểu thức \(B = \left( {\dfrac{{\sqrt x }}{{\sqrt x + 4}} + \dfrac{4}{{\sqrt x – 4}}} \right):\dfrac{{x + 16}}{{\sqrt x + 2}}\) (với \(x \ge 0,x \ne 16\)).
3)Với các biểu thức \(A,B\)nói trên, hãy tìm các giá trị nguyên của \(x\) để giá trị của biểu thức \(P = B\left( {A – 1} \right)\)là số nguyên.
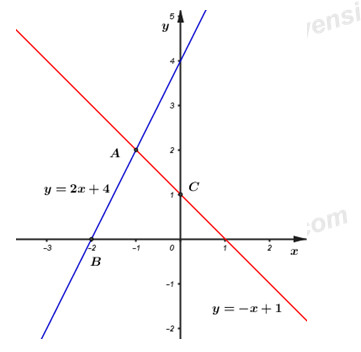
Bài 3: (1,5đ) Cho hàm số \(y = 2x + 4\) có đồ thị là \(\left( {{d_1}} \right)\)và hàm số \(y = – x + 1\) có đồ thị là \(\left( {{d_2}} \right)\)
1)Vẽ \(\left( {{d_1}} \right)\)và \(\left( {{d_2}} \right)\) trên cùng một mặt phẳng tọa độ .
2)Gọi A là giao điểm của \(\left( {{d_1}} \right)\)và \(\left( {{d_2}} \right)\). Tìm tọa độ của điểm A.
3)Xác định các hệ số \(a,b\) của đường thẳng \({d_3}:y = ax + b\). Biết rằng \(\left( {{d_3}} \right)\)song song với \(\left( {{d_1}} \right)\) và \(\left( {{d_3}} \right)\)cắt \(\left( {{d_2}} \right)\) tại một điểm có hoành độ bằng 2.
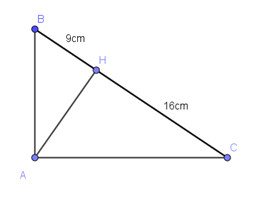
Bài 4: (4,5đ) 1)Cho tam giác ABC vuông tại A có AH là đường cao. Biết \(BH = 9\)cm, \(HC = 16\)cm. Tính độ dài AH, AC, số đo \(\angle ABC\) (số đo làm tròn đến độ).
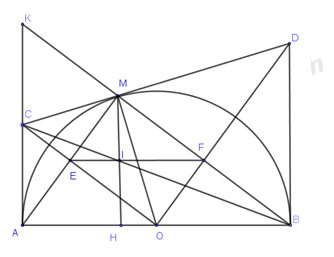
2)Cho nửa đường tròn tâm O đường kính AB. Trên nửa mặt phẳng bờ AB chứa nửa đường tròn, kẻ hai tiếp tuyến Ax, By với nửa đường tròn, M là một điểm nằm trên nửa đường tròn ( M khác A và B), từ M kẻ tiếp tuyến với nửa đường tròn cắt Ax, By lần lượt tại C và D.
a)Chứng minh rằng: \(CD = AC + BD\)
b)AM cắt OCtại E, BM cắt OD tại F. Chứng minh \(EF = OM\).
c)Chứng minh rằng tích \(AC.BD\) không phụ thuộc vào vị trí của điểm M.
d)Kẻ MH vuông góc với AB tại H, MHcắtBCtại I. Chứng minh rằng I là trung điểm của MH.
Bài 5: (0,5đ) Cho \(a,b,c\)là các số dương thỏa mãn điều kiện \(a + b + c + ab + bc + ca = 6\). Chứng minh rằng: \(\dfrac{{{a^3}}}{b} + \dfrac{{{b^3}}}{c} + \dfrac{{{c^3}}}{a} \ge {a^2} + {b^2} + {c^2} \ge 3\)
Bài 1: Thực hiện phép tính:
\(\begin{array}{l}1)\;\;A = \sqrt {12} – 2\sqrt {48} + \dfrac{7}{5}\sqrt {75} \\\;\;\; = \sqrt {{2^2}.3} – 2\sqrt {{4^2}.3} + \dfrac{7}{5}\sqrt {{5^2}.3} \\\;\;\; = 2\sqrt 3 – 2.4\sqrt 3 + \dfrac{7}{5}.5\sqrt 3 = \sqrt 3 .\end{array}\)
Vậy \(A = \sqrt 3 \).\(\)
\(\begin{array}{l}2)\;\;B = \sqrt {14 – 6\sqrt 5 } + \sqrt {{{\left( {2 – \sqrt 5 } \right)}^2}} \\\;\;\;\;\;\;\; = \sqrt {{3^2} + 2.3.\sqrt 5 + {{\left( {\sqrt 5 } \right)}^2}} + \sqrt {{{\left( {2 – \sqrt 5 } \right)}^2}} \\\;\;\;\;\;\;\; = \sqrt {{{\left( {3 + \sqrt 5 } \right)}^2}} + \sqrt {{{\left( {2 – \sqrt 5 } \right)}^2}} \\\;\;\;\;\;\;\; = \left| {3 + \sqrt 5 } \right| + \left| {2 – \sqrt 5 } \right|\\\;\;\;\;\;\;\; = 3 + \sqrt 5 + \sqrt 5 – 2\; = 2\sqrt {5 + 1} .\;\;\;\left( {do\;\;\;\sqrt 5 – 2 > 0} \right)\end{array}\)
Vậy \(B = 2\sqrt 5 + 1\)
Bài 2: 1)Cho biểu thức \(A = \dfrac{{\sqrt x + 4}}{{\sqrt x + 2}}\left( {x \ge 0} \right)\). Tính giá trị biểu thức \(A\) khi \(x = 36\).
Thay \(x = 36\) vào biểu thức ta có: \(A = \dfrac{{\sqrt {36} + 4}}{{\sqrt {36} + 2}} = \dfrac{{6 + 4}}{{6 + 2}} = \dfrac{5}{4}\).
Vậy khi \(x = 36\)thì \(A = \dfrac{5}{4}\).\(\)
2)Rút gọn biểu thức \(B = \left( {\dfrac{{\sqrt x }}{{\sqrt x + 4}} + \dfrac{4}{{\sqrt x – 4}}} \right):\dfrac{{x + 16}}{{\sqrt x + 2}}\) (với \(x \ge 0,x \ne 16\)).
ĐKXĐ: \(x \ge 0,x \ne 16\)
\(\begin{array}{l}B = \left( {\dfrac{{\sqrt x }}{{\sqrt x + 4}} + \dfrac{4}{{\sqrt x – 4}}} \right):\dfrac{{x + 16}}{{\sqrt x + 2}}\\\;\;\; = \left( {\dfrac{{\sqrt x \left( {\sqrt x – 4} \right)}}{{\left( {\sqrt x + 4} \right)\left( {\sqrt x – 4} \right)}} + \dfrac{{4\left( {\sqrt x + 4} \right)}}{{\left( {\sqrt x + 4} \right)\left( {\sqrt x – 4} \right)}}} \right):\dfrac{{x + 16}}{{\sqrt x + 2}}\\\;\;\; = \dfrac{{x – 4\sqrt x + 4\sqrt x + 16}}{{{{\left( {\sqrt x } \right)}^2} – {4^2}}}.\dfrac{{\sqrt x + 2}}{{x + 16}} = \dfrac{{\sqrt x + 2}}{{x – 16}}\end{array}\)
Vậy \(B = \dfrac{{\sqrt x + 2}}{{x – 16}}\).
3)Với các biểu thức \(A,B\)nói trên, hãy tìm các giá trị nguyên của \(x\) để giá trị của biểu thức \(P = B\left( {A – 1} \right)\)là số nguyên.
ĐKXĐ: \(x \ge 0,x \ne 16\). Với điều kiện trên ta có:
\(P = B\left( {A – 1} \right) = \dfrac{{\sqrt x + 2}}{{x – 16}}.\left( {\dfrac{{\sqrt x + 4}}{{\sqrt x + 2}} – 1} \right) = \dfrac{{\sqrt x + 2}}{{x – 16}}.\dfrac{{\sqrt x + 4 – \left( {\sqrt x + 2} \right)}}{{\sqrt x + 2}} = \dfrac{2}{{x – 16}}.\)
Để biểu thức \(P\) nguyên thì \(x – 16\) phải là ước của 2
\( \Rightarrow \left\{ \begin{array}{l}x \ge 0,x \ne 16\\\left[ \begin{array}{l}x – 16 = 2\\x – 16 = – 2\\x – 16 = 1\\x – 16 = – 1\end{array} \right.\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 0,x \ne 16\\\left[ \begin{array}{l}x = 18\\x = 14\\x = 15\\x = 17\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 18\\x = 14\\x = 15\\x = 17\end{array} \right.\)
Vậy với \(x = 18,x = 17,x = 15,x = 14\) thì giá trị của biểu thức \(P = B\left( {A – 1} \right)\)là số nguyên.
Bài 3: Cho hàm số \(y = 2x + 4\) có đồ thị là \(\left( {{d_1}} \right)\)và hàm số \(y = – x + 1\) có đồ thị là \(\left( {{d_2}} \right)\)
1)Vẽ \(\left( {{d_1}} \right)\)và \(\left( {{d_2}} \right)\) trên cùng một mặt phẳng tọa độ .
+) Nhận thấy hai điểm \(A\left( { – 1;2} \right),B\left( { – 2;0} \right)\) thuộc đồ thị hàm số \(y = 2x + 4\).
+) Nhận thấy hai điểm \(A\left( { – 1;2} \right),C\left( {0;1} \right)\)thuộc đồ thị hàm số \(y = – x + 1\).
Từ đó ta có đồ thị của hai hàm số:
2)Gọi A là giao điểm của \(\left( {{d_1}} \right)\)và \(\left( {{d_2}} \right)\). Tìm tọa độ của điểm A.
Hoành độ giao điểm của \(\left( {{d_1}} \right)\)và \(\left( {{d_2}} \right)\)là nghiệm của phương trình:
\(2x + 4 = – x + 1 \Leftrightarrow 3x = – 3 \Leftrightarrow x = – 1\)
Với \(x = – 1 \Rightarrow y = 2x + 4 = 2.\left( { – 1} \right) + 4 = 2\)
Vậy giao điểm của \(\left( {{d_1}} \right)\)và \(\left( {{d_2}} \right)\) là \(A\left( { – 1;2} \right)\)\(\)
3)Xác định các hệ số \(a,b\) của đường thẳng \({d_3}:y = ax + b\). Biết rằng \(\left( {{d_3}} \right)\)song song với \(\left( {{d_1}} \right)\) và \(\left( {{d_3}} \right)\)cắt \(\left( {{d_2}} \right)\) tại một điểm có hoành độ bằng 2.
Vì \(\left( {{d_3}} \right)\)song song với \(\left( {{d_1}} \right)\)nên hai đường thẳng này có hệ số góc bằng nhau\( \Rightarrow \left\{ \begin{array}{l}a = 2\\b \ne 4\end{array} \right..\)
Điểm thuộc \(\left( {{d_2}} \right)\) có hoành độ bằng 2 là \(\left( {2; – 1} \right)\). Vì \(\left( {{d_3}} \right)\)cắt \(\left( {{d_2}} \right)\) tại một điểm có hoành độ bằng 2 nên điểm\(\left( {2; – 1} \right)\) thuộc đồ thị hàm số \({d_3}:y = ax + b\)
\(\begin{array}{l} \Rightarrow – 1 = a.2 + b\\ \Rightarrow b = – 1 – 2a = – 1 – 2.2 = – 5\;\;\left( {tm} \right)\end{array}\)
Vậyb\(a = 2,b = – 5\).
Bài 4: (4,5đ) 1)Cho tam giác ABC vuông tại A có AH là đường cao. Biết \(BH = 9\)cm, \(HC = 16\)cm. Tính độ dài AH, AC, số đo \(\angle ABC\) (số đo làm tròn đến độ).
Xét tam giác ABC vuông tại A có AH là đường cao.
Áp dụng hệ thức lượng trong tam giác vuông ta có:
\(\begin{array}{l} + )A{H^2} = BH.HC \Rightarrow AH = \sqrt {9.16} = 12\\ + )A{C^2} = CH.BC = CH.\left( {CH + BH} \right) \Rightarrow AC = \sqrt {16.\left( {9 + 16} \right)} = 20\end{array}\)
Xét tam giác ABC vuông tại A có:
\(\sin \left( {\angle ABC} \right) = \dfrac{{AC}}{{BC}} = \dfrac{{AC}}{{CH + BH}} = \dfrac{{20}}{{16 + 9}} = \dfrac{4}{5} \Rightarrow \angle ABC = \arcsin \dfrac{4}{5} \approx {53^o}\).
2)Cho nửa đường tròn tâm O đường kính AB. Trên nửa mặt phẳng bờ AB chứa nửa đường tròn, kẻ hai tiếp tuyến Ax, By với nửa đường tròn, M là một điểm nằm trên nửa đường tròn ( M khác A và B), từ M kẻ tiếp tuyến với nửa đường tròn cắt Ax, By lần lượt tại C và D.
a)Chứng minh rằng: \(CD = AC + BD\)
Xét nửa đường tròn tâm O đường kính AB có AC và MC là hai tiếp tuyến giao nhau tại M với M,A là tiếp điểm\( \Rightarrow AC = MC\)(tính chất tiếp tuyến)
Chứng minh tương tự ta có\(MD = BD\).
Vì M nằm trên đoạn CD nên\(CD = MD + MC\). Mà có\(AC = CM,BD = MD\) (cmt)
Suy ra \(CD = AC + BD\) (đpcm).\(\)\(\)\(\)
b)AM cắt OC tại E, BM cắt OD tại F. Chứng minh \(EF = OM\).
Có:\(MD = BD\)(cmt) suy ra D nằm trên đường trung trực của MB (do cách đều hai điểm M, B)
Có: \(OM = OB\)(do cùng là bán kính) suy ra O nằm trên trung trực của MB (do cách đều M, B)
Suy ra OD là trung trực của MB, suy ra \(OD \bot MB.\)
Chứng minh tương tự có \(OC \bot AM.\)
Xét tứ giác MEOF có:
+) \(\angle AMB = {90^o}\) (góc nội tiếp chắn nửa đường tròn)
+) \(\angle MEO = {90^o}\) (do \(OC \bot AM\))
+) \(\angle MFO = {90^o}\)(do \(OD \bot MB\))
Suy ra tứ giác MEOF là hình chữ nhật (do có 3 góc vuông), suy ra \(EF = MO\)(hình chữ nhật có hai đường chéo bằng nhau). (đpcm)
c)Chứng minh rằng tích \(AC.BD\) không phụ thuộc vào vị trí của điểm M.
Vì MEOF là hình chữ nhật nên\(\angle FOE = {90^o}\), suy ra tam giác CODvuông tại O.
Xét tam giác COD vuông tại O có OMlà đường cao (\(OM \bot CD\)do CD là tiếp tuyến với đường tròn)
\( \Rightarrow CM.MD = O{M^2}\)(hệ thức lượng trong tam giác vuông)
Mà có: \(CM = AC,\;\;MD = BD\)(cmt)
\( \Rightarrow AC.BD = O{M^2} = {R^2}\).
\( \Rightarrow AC.BD\)luôn không đổi với mọi vị trí của điểm M.
d)Kẻ MHvuông góc với ABtại H, MH cắt BC tạiI. Chứng minh rằng Ilà trung điểm của MH.
Kéo dài MB cắt AC tại K.
Có: \(\angle CKM = \angle DBM\)(do AC song song với BD) (1)
Có: \(\angle KMC = \angle DMB\)(hai góc đối đỉnh) (2)
Mà có tam giác MBD cân tại D (do \(MD = BD\)) nên \(\angle DMB = \angle DBM\) (3)
Từ (1), (2), (3) ta có: \(\angle CKM = \angle KMC\), suy ra tam giác KMC cân tại C, suy ra \(KC = CM\).
Mà có: \(CA = CM\) (cmt)
\( \Rightarrow CK = AC = \dfrac{1}{2}AK\).
Xét tam giác KBC có: MI song song với KC (do cùng vuông góc với AB)
\( \Rightarrow \dfrac{{MI}}{{KC}} = \dfrac{{BM}}{{BK}}\) (định lí Ta-lét) (4)
Xét tam giác ABK có MH song song với AK (do cùng vuông góc với AB)
\( \Rightarrow \dfrac{{MH}}{{AK}} = \dfrac{{BM}}{{BK}}\) (định lí Ta-lét) (5)
Từ (4) và (5) suy ra \(\dfrac{{MI}}{{KC}} = \dfrac{{MH}}{{AK}}\). Mà có \(KC = \dfrac{1}{2}AK\) (cmt)
\( \Rightarrow MI = \dfrac{1}{2}MH \Rightarrow IH = MH – MI = MH – \dfrac{1}{2}MH = \dfrac{1}{2}MH \Rightarrow MH = MI\)
Vậy I là trung điểm của IH (đpcm).
Bài 5: Cho \(a,b,c\)là các số dương thỏa mãn điều kiện \(a + b + c + ab + bc + ca = 6\). Chứng minh rằng: \(\dfrac{{{a^3}}}{b} + \dfrac{{{b^3}}}{c} + \dfrac{{{c^3}}}{a} \ge {a^2} + {b^2} + {c^2} \ge 3\).
+) Chứng minh bất đẳng thức phụ: Với \(a,b,c\)là các số dương ta có:
\(\left\{ \begin{array}{l}\dfrac{{{a^2}}}{2} + \dfrac{{{b^2}}}{2} \ge 2\sqrt {\dfrac{{{a^2}}}{2}.\dfrac{{{b^2}}}{2}} = ab\\\dfrac{{{b^2}}}{2} + \dfrac{{{c^2}}}{2} \ge 2\sqrt {\dfrac{{{b^2}}}{2}.\dfrac{{{c^2}}}{2}} = bc\\\dfrac{{{c^2}}}{2} + \dfrac{{{a^2}}}{2} \ge 2\sqrt {\dfrac{{{c^2}}}{2}.\dfrac{{{a^2}}}{2}} = ac\end{array} \right.\) \( \Rightarrow 2\left( {\dfrac{{{a^2}}}{2} + \dfrac{{{b^2}}}{2} + \dfrac{{{c^2}}}{2}} \right) \ge ab + bc + ca \Rightarrow {a^2} + {b^2} + {c^2} \ge ab + bc + ca\)
Từ bất đẳng thức trên ta dễ chứng minh được bất đẳng thức thứ hai.
Ta có: \(\begin{array}{l}\;\;\;\;{a^2} + {b^2} + {c^2} \ge ab + bc + ca\\ \Leftrightarrow {a^2} + {b^2} + {c^2} + 2ab + 2bc + 2ca \ge 3\left( {ab + bc + ca} \right)\\ \Leftrightarrow {\left( {a + b + c} \right)^2} \ge 3\left( {ab + bc + ca} \right)\end{array}\)
+) Xét bất đẳng thức \(\dfrac{{{a^3}}}{b} + \dfrac{{{b^3}}}{c} + \dfrac{{{c^3}}}{a} \ge {a^2} + {b^2} + {c^2}\)\(\)
Áp dụng bất đẳng thức Co-si ta có:
\(\begin{array}{l} + )\dfrac{{{a^3}}}{b} + ab \ge 2\sqrt {\dfrac{{{a^3}}}{b}.ab} = 2{a^2}\\ + )\dfrac{{{b^3}}}{c} + bc \ge 2\sqrt {\dfrac{{{b^3}}}{c}.bc} = 2{b^2}\\ + )\dfrac{{{c^3}}}{a} + ac \ge 2\sqrt {\dfrac{{{c^3}}}{a}.ac} = 2{c^2}\\ \Rightarrow \dfrac{{{a^3}}}{b} + \dfrac{{{b^3}}}{c} + \dfrac{{{c^3}}}{a} \ge 2\left( {{a^2} + {b^2} + {c^2}} \right) – \left( {ab + bc + ca} \right) = {a^2} + {b^2} + {c^2} + \left[ {{a^2} + {b^2} + {c^2} – \left( {ab + bc + ca} \right)} \right]\end{array}\)
Mà có: \({a^2} + {b^2} + {c^2} \ge ab + bc + ca \Rightarrow {a^2} + {b^2} + {c^2} – \left( {ab + bc + ca} \right) \ge 0\)
\(\begin{array}{l} \Rightarrow {a^2} + {b^2} + {c^2} + \left( {{a^2} + {b^2} + {c^2} – \left( {ab + bc + ca} \right)} \right) \ge {a^2} + {b^2} + {c^2}\\ \Rightarrow \dfrac{{{a^3}}}{b} + \dfrac{{{b^3}}}{c} + \dfrac{{{c^3}}}{a} \ge {a^2} + {b^2} + {c^2}\end{array}\)
Xét bất đẳng thức: \({a^2} + {b^2} + {c^2} \ge 3\)
Theo đề bài có: \(a + b + c + ab + bc + ca = 6\)
Mà có: \(ab + bc + ca \le \dfrac{{{{\left( {a + b + c} \right)}^2}}}{3}\) (cmt)
\(\begin{array}{l} \Rightarrow \left( {a + b + c} \right) + \dfrac{{{{\left( {a + b + c} \right)}^2}}}{3} \ge 6 \Leftrightarrow {\left( {a + b + c} \right)^2} + 3\left( {a + b + c} \right) – 18 \ge 0\\ \Leftrightarrow \left( {a + b + c – 3} \right)\left( {a + b + c + 6} \right) \ge 0 \Leftrightarrow a + b + c \ge 3\end{array}\)
Do \(a,b,c > 0 \Rightarrow a + b + c + 6 > 0\)
Áp dụng bất đẳng thức Bunhiacopski cho bộ ba số \(\left( {1;1;1} \right)\) và \(\left( {a;b;c} \right)\) có:
\(\left( {{1^2} + {1^2} + {1^2}} \right)\left( {{a^2} + {b^2} + {c^2}} \right) \ge {\left( {a.1 + b.1 + c.1} \right)^2} \Leftrightarrow {a^2} + {b^2} + {c^2} \ge \dfrac{{{{\left( {a + b + c} \right)}^2}}}{3} \ge \dfrac{{{3^2}}}{3} = 3\).
Vậy ta chứng minh được \(\dfrac{{{a^3}}}{b} + \dfrac{{{b^3}}}{c} + \dfrac{{{c^3}}}{a} \ge {a^2} + {b^2} + {c^2} \ge 3\).