Đề bài
Tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau. Gọi M, N, L lần lượt là trung điểm của AB, AD và đường chéo AC. Từ M kẻ đường thẳng vuông góc với CD cắt AC tại H.
Chứng minh rằng: H là trực tâm của tam giác MNL.
Phương pháp giải - Xem chi tiết
Sử dụng:
- Định nghĩa: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
- Định lí : Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
- Trực tâm của tam giác là giao ba đường cao của tam giác đó.
Lời giải chi tiết
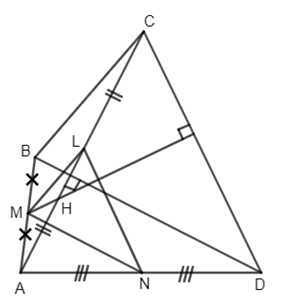
Ta có \(AC \bot BD\) (giải thiết) hay \(HL \bot BD\)
Mà \(MN// BD\) (do MN là đường trung bình của \(\Delta ABD\) ) \( \Rightarrow HL \bot MN(1)\)
Lại có \(MH \bot CD\) (giả thiết)
\(NL// CD\) (do NL là đường trung bình của \(\Delta ACD)\)
\( \Rightarrow MH \bot NL\left( 2 \right)\)
Từ (1) và (2) ta có H là giao điểm hai đường cao MH và LH của tam giác MNL nên H là trực tâm của \(\Delta MNL.\)
dapandethi.vn
