Đề bài
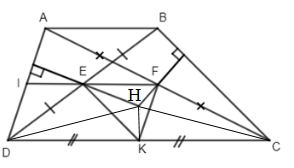
Cho hình thang ABCD \(\left( {AB// CD} \right)\) . Gọi E, F, K lần lượt là trung điểm của BD, AC, DC. Gọi H là giao điểm của đường thẳng qua E vuông góc với AD và đường thẳng qua F vuông góc với BC. Chứng minh rằng:
a) H là trực tâm của \(\Delta EFK.\)
b) \(\Delta HCD\) cân.
Phương pháp giải - Xem chi tiết
Sử dụng:
- Định nghĩa: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
- Định lí : Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
- Trực tâm của tam giác là giao ba đường cao của tam giác đó.
Lời giải chi tiết
a) Ta có E, K lần lượt là trung điểm của BD và CD nên EK là đường trung bình của \(\Delta BCD\)
\( \Rightarrow EK//BC\) mà \(HF \bot BC(gt)\)
\( \Rightarrow HF \bot EK.\)
Ta có F, K lần lượt là trung điểm của AC và CD nên FK là đường trung bình của \(\Delta ACD\)
\( \Rightarrow FK//AD\) mà \(EH \bot AD(gt)\)
\( \Rightarrow EH \bot FK.\)
Xét tam giác EFK có hai đường cao EH và FH cắt nhau tại H
Do đó H là trực tâm của \(\Delta EFK.\)
b) Gọi I là trung điểm của AD, ta có IE là đường trung bình của \(\Delta ABD\)
\( \Rightarrow IE// AB// CD\) (1)
Và IF là đường trung bình của \(\Delta ACD \Rightarrow IF// DC\) (2)
Từ (1) và (2) \( \Rightarrow \) IE và IF phải trùng nhau (tiên đề Ơ clit) hay ba điểm I, E, F thẳng hàng.
Hay \(EF// DC\) mà \(KH \bot EF\) (H là trực tâm \(\Delta EFK\) )\( \Rightarrow KH \bot DC.\)
Vì vậy xét \(\Delta DHC\) có đường trung tuyến HK đồng thời là đường cao nên \(\Delta DHC\) cân tại H.
dapandethi.vn