Đề bài
Bài 1. Tìm a, b để đa thức \(A\left( x \right) = 2{x^3} + 7{x^2} + ax + b\) chia hết cho đa thức \(B\left( x \right) = {x^2} + x - 1.\)
Bài 2. Tìm a để phép chia \(A\left( x \right) = 2{x^2} - x + a\) cho \(B(x) = 2x - 5\) có dư bằng \( - 10.\)
Phương pháp giải - Xem chi tiết
Đặt phép tính chia theo hàng dọc
Phép chia hết có số dư bằng 0.
Lời giải chi tiết
1.
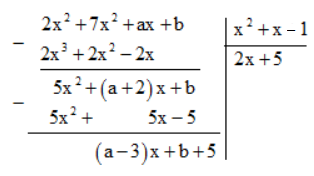
Phép chia trên có phần dư là \(\left( {a - 3} \right)x + b + 5\).
A(x) chia hết cho B(x) khi \(\left( {a - 3} \right)x + b + 5\) là đa thức 0.
Suy ra \(a-3=0\) và \(b+5=0\)
Hay \(a=3\) và \(b=-5\)
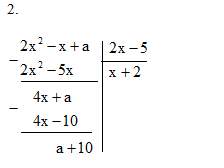
A(x) cho cho B(x) có dư bằng \( a + 10\)
Theo đề bài, ta có:
\( a + 10 = - 10 \Rightarrow a = - 20.\)
dapandethi.vn
