Đề bài
Cho hình bình hành ABCD. Trên đường chéo BD lấy hai điểm M và N sao cho DM = MN = NB. Gọi O là giao điểm của hai đường chéo AC và BD.
a) Chứng minh rằng M và N đối xứng với nhau qua O.
b) Gọi P, Q lần lượt là giao điểm của AM và CN với các cạnh DC và AB. Chứng minh rằng P và Q đối xứng nhau qua O.
Phương pháp giải - Xem chi tiết
Sử dụng:
Hai đường chéo của hình bình hành giao nhau tại trung điểm mỗi đường
Hai điểm gọi là đối xứng với nhau qua điểm \(O\) nếu \(O\) là trung điểm của đoạn thẳng nối hai điểm đó.
Tứ giác có hai đường chéo giao nhau tại trung điểm của mỗi đường là hình bình hành
Tứ giác có hai cặp cạnh đối song song là hình bình hành
Lời giải chi tiết
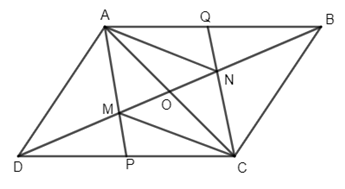
a) Ta có: OB = OD (tính chất hai đường chéo của hình bình hành ABCD)
BN = DM (gt)
\( \Rightarrow OB - BN = OD - DM\)
\( \Rightarrow ON = OM\) hay O là trung điểm MN chứng tỏ M và N đối xứng nhau qua O.
b) Tứ giác ANCM có OM = ON (cmt)
OA = OC (gt)
\( \Rightarrow ANCM\) là hình bình hành (hai đường chéo cắt nhau tại trung điểm mỗi đường) \( \Rightarrow AM// CN\) hay \(AP// CQ\) lại có \(AQ//CP.\) Do đó AQCP là hình bình hành (các cạnh đối song song) mà O là trung điểm của đường chéo AC nên đường chéo thứ hai PQ phải qua O hay OP = OQ.
Chứng tỏ P và Q đối xứng nhau qua O.
dapandethi.vn
