Đề bài
Trong các hình vẽ sau, hình nào có tâm đối xứng ?
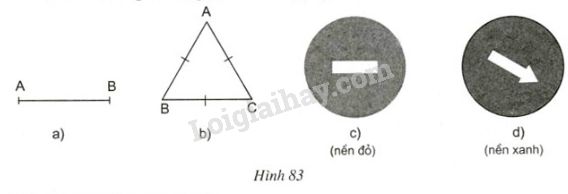
a) Đoạn thẳng \(AB\) (h.\(83a\));
b) Tam giác đều \(ABC\) (h.\(83b\));
c) Biển cấm đi ngược chiều (h.\(83c\));
d) Biển chỉ hướng đi vòng tránh chướng ngại vật (h.\(83d\))
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng định nghĩa: Hình có tâm đối xứng
Điểm \(O\) gọi là tâm đối xứng qua hình \(H\) nếu điểm đối xứng với mỗi điểm thuộc hình \(H\) qua điểm \(O\) cũng thuộc hình \(H.\)
Lời giải chi tiết
- Hình \(83a\) có tâm đối xứng là trung điểm của đoạn thẳng \(AB\).
- Hình \(83b\) không có tâm đối xứng.
Giải thích: Nếu gọi \(O\) là giao điểm của \(3\) đường trung trực trong \(ΔABC\) (là tam giác đều) thì điểm đối xứng của \(3\) điểm \(A, B, C\) qua \(O\) không thuộc \(ΔABC\) \(\Rightarrow \) Hình này không có tâm đối xứng.
- Hình \(83c\) có tâm đối xứng là tâm của đường tròn.
- Hình \(83d\) không có tâm đối xứng.
Giải thích: Nếu gọi \(O\) là tâm đường tròn. Thì có vô số điểm thuộc hình dấu "\( \Rightarrow \)" sẽ không có điểm đối xứng thuộc hình dấu "\( \Rightarrow \)" nên hình này cũng không có tâm đối xứng.
dapandethi.vn
