Đề bài
Cho tam giác ABC, các trung tuyến BM và CN. Gọi D là điểm đối xứng với B qua M, E là điểm đối xứng với C qua N. Chứng minh rằng D đối xứng với E qua A.
Phương pháp giải - Xem chi tiết
Sử dụng:
Hai điểm gọi là đối xứng với nhau qua điểm \(O\) nếu \(O\) là trung điểm của đoạn thẳng nối hai điểm đó.
Tứ giác có hai đường chéo giao nhau tại trung điểm của mỗi đường là hình bình hành.
Lời giải chi tiết
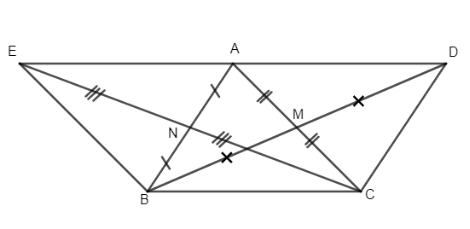
Ta có N là trung điểm của AB (gt); N là trung điểm của EC (tính chất đối xứng)
Do đó EABC là hình bình hành (do có hai đường chéo AB và EC giao nhau tại trung điểm N của mỗi đường)
\( \Rightarrow EA//BC\;\;\left( 1 \right)\) và EA = BC.
Ta có M là điểm trung điểm của AC (gt); M là trung điểm của BD (tính chất đối xứng)
Do đó ADCB là hình bình hành (do có hai đường chéo AC và BD giao nhau tại trung điểm M của mỗi đường)
\( \Rightarrow AD//BC\left( 2 \right)\) và AD = BC.
Từ (1) và (2) \( \Rightarrow EA\) và DA phải trùng nhau (tiên đề Ơ clit) hay ba điểm E, A, D thẳng hàng và AE = AD chứng tỏ D đối xứng với E qua A.
dapandethi.vn
