Bài 1: (2đ) a) Tính chu vi tam giác ABC biết độ dài 3 cạnh là \(AB = 5\sqrt 2 \left( {cm} \right),AC = \sqrt {32} \left( {cm} \right)\),\(BC = \sqrt {98} \left( {cm} \right)\). (Không yêu cầu vẽ hình)
b) Thu gọn: \(B = \sqrt {{{\left( {\sqrt 7 – 1} \right)}^2}} – \dfrac{6}{{\sqrt 7 – 1}}\).
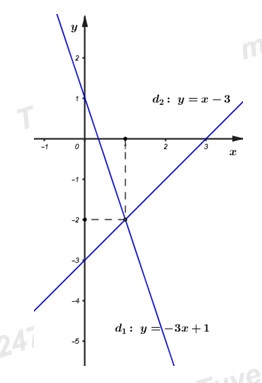
Bài 2: (3,0đ) Cho đường thẳng \(\left( {{d_1}} \right):y = – 3x + 1\) và đường thẳng \(\left( {{d_2}} \right):y = x – 3\).
a)Vẽ \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) trên cùng mặt phẳng tọa độ \(Oxy\).
b)Tìm tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) bằng phép tính.
c)Tìm \(m\) để đường thẳng \(\left( D \right):y = \left( {2m + 3} \right)x – 5\) song song vơi đường thẳng \(\left( {{d_1}} \right)\).
Bài 3: (1đ) Trong một tòa nhà ngoài thang máy người ta còn xây thêm một cầu thang đi bộ. Từ tầng 1 đến tầng 2 có 30 bậc thang. Các tầng còn lại cứ hai tầng liên tiếp cách nhau 21 bậc thang. Do thang máy bị hư nên bạn Vy đi bộ bắt đầu từ tầng 1 về căn hộ của mình. Tổng số bậc thang Vy đã đi là 135. Hỏi căn hộ của Vy ở tầng thứ bao nhiêu của tòa nhà?
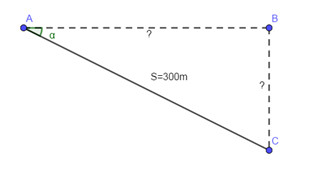
Bài 4: (1đ) Tàu ngầm đang ở trên mặt biển bỗng đột ngột lặn xuống theo phương tạo với mặt nước biển một góc\({21^o}\). Nếu tàu chuyển động theo phương lặn xuống được 300m thì nó ở độ sâu bao nhiêu? Khi đó khoảng cách theo phương nằm ngang so với nơi xuất phát là bao nhiêu mét ? (kết quả làm tròn đến mét)
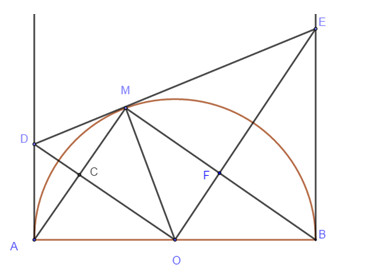
Bài 5: (3,0đ) Cho nửa đường tròn \(\left( {O;R} \right)\) đường kính AB. Vẽ các tiếp tuyến \(Ax\) và \(By\) của đường tròn \(\left( {O;R} \right)\).
a)Chứng minh: \(Ax//By\).
b)Trên \(\left( {O;R} \right)\)lấy điểm M. Tiếp tuyến tại M của đường tròn \(\left( {O;R} \right)\)lần lượt cắt \(Ax\) và \(By\) tại D và E. Chứng minh: \(DE = DA + BE\).
c)Chứng minh: \(\angle DOE = {90^o}\) và \(DA.BE = {R^2}\).
Bài 1: a)Tính chu vi tam giác ABC biết độ dài 3 cạnh là \(AB = 5\sqrt 2 \left( {cm} \right),AC = \sqrt {32} \left( {cm} \right)\),\(BC = \sqrt {98} \left( {cm} \right)\). (Không yêu cầu vẽ hình)
Chu vi của tam giác ABC là:
\(\begin{array}{l}AB + AC + BC = 5\sqrt 2 + \sqrt {32} + \sqrt {98} = 5\sqrt 2 + \sqrt {{4^2}.2} + \sqrt {{7^2}.2} \\ = 5\sqrt 2 + 4\sqrt 2 + 7\sqrt 2 = 16\sqrt 2 .\end{array}\)
Vậy tam giác có chu vi là \(16\sqrt 2 \).\(\)
b)Thu gọn: \(B = \sqrt {{{\left( {\sqrt 7 – 1} \right)}^2}} – \dfrac{6}{{\sqrt 7 – 1}}\).
\(\begin{array}{l}B = \sqrt {{{\left( {\sqrt 7 – 1} \right)}^2}} – \dfrac{6}{{\sqrt 7 – 1}} \\\;\;\;= \left| {\sqrt 7 – 1} \right| – \dfrac{{6\left( {\sqrt 7 + 1} \right)}}{{\left( {\sqrt 7 – 1} \right)\left( {\sqrt 7 + 1} \right)}}\\\;\;\; = \sqrt 7 – 1 – \dfrac{{6\left( {\sqrt 7 + 1} \right)}}{{{{\left( {\sqrt 7 } \right)}^2} – 1}} \\\;\;\;= \sqrt 7 – 1 – \left( {\sqrt 7 + 1} \right)\\\;\;\; = \sqrt 7 – 1 – \sqrt 7 – 1 = – 2.\end{array}\)
Vậy \(B = – 2\).
Bài 2:Cho đường thẳng \(\left( {{d_1}} \right):y = – 3x + 1\) và đường thẳng \(\left( {{d_2}} \right):y = x – 3\).
a)Vẽ \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) trên cùng mặt phẳng tọa độ \(Oxy\).
Ta có bảng giá trị:
|
x |
0 |
1 |
|
\(y = – 3x + 1\) |
1 |
-2 |
|
\(y = x – 3\) |
-3 |
-2 |
Vậy đường thẳng \(\left( {{d_1}} \right)\) đi qua điểm \(\left( {0;\;1} \right),\;\;\left( {1; – 2} \right)\) và đường thẳng \(\left( {{d_2}} \right)\) đi qua điểm \(\left( {0; – 3} \right),\;\;\left( {1; – 2} \right).\)
Từ đó ta có đồ thị của hai hàm số:
b)Tìm tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) bằng phép tính.
Hoành độ giao điểm của hai đường thẳng là nghiệm của phương trình :
\( – 3x + 1 = x – 3 \Leftrightarrow 4x = 4 \Leftrightarrow x = 1\).
Với \(x = 1 \Rightarrow y = x – 3 = 1 – 3 = – 2\)
Vậy tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\)là: \(A\left( {1; – 2} \right)\).\(\)
c)Tìm \(m\) để đường thẳng \(\left( D \right):y = \left( {2m + 3} \right)x – 5\) song song với đường thẳng \(\left( {{d_1}} \right)\).
Hai đường thẳng song song khi chúng có cùng hệ số góc và chúng không trùng nhau. Suy ra để
đường thẳng \(\left( D \right):y = \left( {2m + 3} \right)x – 5\) song song với đường thẳng \(\left( {{d_1}} \right)\) thì:
\(\left\{ \begin{array}{l}2m + 3 = – 3\\ – 5 \ne 1\end{array} \right. \)
\(\Leftrightarrow \left\{ \begin{array}{l}2m = – 6\\ – 5 \ne 1\end{array} \right. \Leftrightarrow m = – 3\).
Vậy \(m = – 3\) là giá trị cần tìm.
Bài 3:Trong một tòa nhà ngoài thang máy người ta còn xây thêm một cầu thang đi bộ. Từ tầng 1 đến tầng 2 có 30 bậc thang. Các tầng còn lại cứ hai tầng liên tiếp cách nhau 21 bậc thang. Do thang máy bị hư nên bạn Vy đi bộ bắt đầu từ tầng 1 về căn hộ của mình. Tổng số bậc thang Vy đã đi là 135. Hỏi căn hộ của Vy ở tầng thứ bao nhiêu của tòa nhà?
Giả sử nhà bạn Vy ở tầng thứ \(n\) của tòa nhà\(\left( {n > 1,\;n \in {N^*}} \right).\)
Suy ra sốtầng mà bạn Vy phải đi là \(n – 1\)tầng.
\( \Rightarrow \)số tầng mà bạn Vy phải đi có 21 bậc thang là: \(n – 2\) (do cầu thang tầng 1 có 30 bậc thang)
Suy ra số bậc thang mà bạn Vy phải đi bộ là: \(30 + 21.\left( {n – 2} \right)\) bậc.
Theo đề bài ta có phương trình:
\(30 + 21\left( {n – 2} \right) = 135 \Leftrightarrow n – 2 = 5 \Leftrightarrow n = 7\;\;\left( {tm} \right)\).
Vậy nhà bạn Vy ở tầng 7 của tòa nhà.\(\)
Bài 4:Tàu ngầm đang ở trên mặt biển bỗng đột ngột lặn xuống theo phương tạo với mặt nước biển một góc \({21^o}\). Nếu tàu chuyển động theo phương lặn xuống được 300m thì nó ở độ sâu bao nhiêu? Khi đó khoảng cách theo phương nằm ngang so với nơi xuất phát là bao nhiêu mét ? (kết quả làm tròn đến mét)
Coi mặt biển là một mặt phẳng, theo đề bài ta có hình vẽ minh họa:
 Trong hình vẽ ta có:
Trong hình vẽ ta có:
+) Đoạn AC là quãng đường tàu di chuyển trong quá trình lặn,
+) Đoạn BC là độ sâu mà tàu lặn được.
+) Đoạn AB là khoảng cách theo phương ngang tính từ vị trí xuất phát tới vị trí của tàu sau khi lặn.
+) \(\alpha \) là góc tạo bởi quãng đường tàu chuyển động và mặt biển.
Xét tam giác vuông ABC vuông tại B có:
+) \(\sin \alpha = \dfrac{{BC}}{{AC}}\) \( \Rightarrow BC = AC.\sin \alpha = 300.\sin {21^o} \approx 107\left( m \right)\)
+) \(\cos \alpha = \dfrac{{AB}}{{AC}}\) \( \Rightarrow AB = AC.\cos \alpha = 300.cos{21^o} = 280\left( m \right)\)
Vậy tàu lặn xuống độ sâu 107 (m) và khoảng cách theo phương ngang từ vị trí ban đầu tới vị trí sau khi lặn là 280 (m).
Bài 5:Cho nửa đường tròn \(\left( {O;R} \right)\) đường kính AB. Vẽ các tiếp tuyến \(Ax\) và \(By\) của đường tròn \(\left( {O;R} \right)\).
a)Chứng minh: \(Ax//By\).
Xét đường tròn \(\left( {O;R} \right)\)có \(Ax\) là tiếp tuyến với A là tiếp điểm.
\( \Rightarrow Ax \bot OA\)(tính chất tiếp tuyến)\( \Rightarrow Ax \bot AB\)(do OA nằm trên AB)\(\)
Chứng minh tương tự có \(By \bot AB\)
Suy ra \(Ax//By\) (do cùng vuông góc với AB)(đpcm).\(\)
b)Trên \(\left( {O;R} \right)\)lấy điểm M. Tiếp tuyến tại M của đường tròn \(\left( {O;R} \right)\)lần lượt cắt \(Ax\) và \(By\) tại D và E. Chứng minh: \(DE = DA + BE\).
Xét \(\left( {O;R} \right)\)có DM, AD là tiếp tuyến với A, Mlà tiếp điểm
\( \Rightarrow AD = DM\)(tính chất tiếp tuyến) (1)
Tương tự ta có: \(ME = BE\) (2)
Vì M nằm trên đoạn DE nên ta có: \(DE = DM + ME\) (3)
Từ (1) , (2) , (3) suy ra\(DE = DA + BE\)(đpcm).
c)Chứng minh: \(\angle DOE = {90^o}\) và \(DA.BE = {R^2}\).
+)Chứng minh \(\angle DOE = {90^o}\)
Có: \(DM = DA\)(cmt), suy ra D cách đều A và M, suy ra D nằm trên đường trung trực của AM
Mà có: \(OA = OM\) (cùng là bán kính) suy ra O cách đều A và M, suy ra O nằm trên trung trực của AM
Suy ra OD là trung trực của AM, suy ra \(OD \bot AM.\)
Chứng minh tương tự có \(OE \bot MB.\)
Xét tứ giác MCOF có:
+) \(\angle MCO = {90^o}\) (do \(OD \bot AM\))
+) \(\angle MFO = {90^o}\)(do \(OE \bot MB\))
+) \(\angle CMF = {90^o}\)(do là góc nội tiếp chắn nửa đường tròn)
Suy ra MCOF là hình chữ nhật (dhnb), suy ra \(\angle DOE = {90^o}\). (đpcm)
+) Chứng minh \(DA.BE = {R^2}\).
Xét tam giác DOE vuông tại O có: OM là đường cao (do DE là tiếp tuyến nên OM vuông góc với DE )
\( \Rightarrow ME.MD = O{M^2}\)
Mà có: \(\left\{ \begin{array}{l}DA = MD\\BE = ME\end{array} \right.\) (cmt)
Suy ra \(DA.BE = {R^2}\) (đpcm).