Đề bài
Cho tam giác ABC có AB = AC, phân giác của góc A cắt BC tại H.
a) Chứng minh rằng \(\Delta AHB = \Delta AHC\)
b) Chứng minh rằng AH vuông góc với BC.
c) Kẻ \(HE \bot AB(E \in AB),HF \bot AC(F \in AC).\) Chứng minh rằng \(\Delta HEB = \Delta HFC\)
d) Trên tia đối của tia HA ta lấy điểm D sao cho H là trung điểm của AD. Chứng minh rằng \(FH \bot BD\)
Lời giải chi tiết
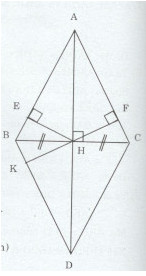
a)Xét tam giác AHB và AHC có:
AB = AC (giả thiết)
\(\widehat {BAH} = \widehat {CAH}\) (AH là tia phân giác của góc BAC)
AH là cạnh chung.
Do đó: \(\Delta AHB = \Delta AHC(c.g.c)\)
b) Ta có: \(\Delta AHB = \Delta AHC\) (chứng minh câu a)
Suy ra: \(\widehat {AHB} = \widehat {AHC};\widehat {ABH} = \widehat {ACH}\)
Mà \(\widehat {AHB} + \widehat {AHC} = {180^0}\) (kề bù)
Nên \(\eqalign{ & \widehat {AHC} + \widehat {AHC} = {180^0} \Rightarrow 2\widehat {AHC} = {180^0}. \cr & \widehat {AHC} = {90^0} \Rightarrow AH \bot BC \cr} \)
c) Tam giác EBH vuông tại E có: \(\widehat {EBH} + \widehat {EHB} = {90^0}\)
Tam giác FHC vuông tại F có: \(\widehat {FHC} + \widehat {FCH} = {90^0}\)
Mà \(\widehat {EBH} = \widehat {FCH}\) (chứng minh câu b) nên \(\widehat {EHB} = \widehat {FHC.}\)
Xét tam giác HEB và HFC có:
\(\eqalign{ & \widehat {EBH} = \widehat {FCH} \cr & \widehat {EHB} = \widehat {FHC}(cmt) \cr & HB = HC(\Delta AHB = \Delta AHC) \cr} \)
Do đó: \(\Delta HEB = \Delta HFC(g.c.g)\)
d) Xét tam giác AHC và DHB có:
AH = DH (giả thiết)
\(\eqalign{ & HC = HB(\Delta AHB = \Delta AHC) \cr & \widehat {AHC} = \widehat {BHD}( = {90^0}) \cr} \)
Do đó: \(\Delta AHC = \Delta DHB(c.g.c) \Rightarrow \widehat {HAC} = \widehat {HDB}\)
Mà hai góc này ở vị trí so le trong do đó AC // BD.
Mặt khác \(HF \bot AC\) (giả thiết) nên ta có: \(HF \bot BD\)
dapandethi.vn
