Đề bài
Cho tam giác ABC nhọn (AC <AC), gọi E là trung điểm của AC. Trên tia đối của tia EB ta lấy điểm M sao cho E là trung điểm của MB.
a) Chứng minh rằng \(\Delta EBC = \Delta EMA\)
b) Chứng minh rằng MA // BC.
c) Gọi F là trung điểm của Ab, trên tia đối của tia FC ta lấy điểm N sao cho F là trung điểm của NC. Chứng minh rằng ba điểm M, A, N thẳng hàng.
Lời giải chi tiết
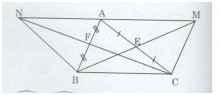
a)Xét tam giác EBC và EMA có:
EC = EA (E là trung điểm AC)
EB = EM (E là trung điểm BM)
\(\widehat {BEC} = \widehat {AEM}\) (hai góc đối đỉnh)
Do đó: \(\Delta EBC = \Delta EMA(c.g.c)\)
b)Ta có: \(\Delta EBC = \Delta EMA\) (chứng minh câu a) \( \Rightarrow \widehat {ECB} = \widehat {EAM}\)
Mà hai góc ECB và EAM ở vị trí so le trong nên MA // BC.
c) Xét tam giác AFN và BFC có:
AF = BF (F là trung điểm của AB)
\(\widehat {AFN} = \widehat {BFC}\) (hai góc đối đỉnh)
FN = FC (F là trung điểm của NC)
Do đó: \(\Delta AFN = \Delta BFC(c.g.c) \Rightarrow \widehat {AFN} = \widehat {BCF}\)
Mà hai góc này ở vị trí so le trong nên AN // BC.
Ta có: MA // BC (chứng minh câu b) và AN // BC (chứng minh trên)
Do đó: MA, AN trùng nhau (theo tiên đề Euclide). Vậy M, A, N thẳng hàng.
dapandethi.vn
