Đề bài
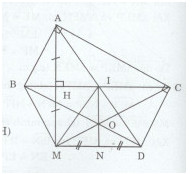
Cho tam giác ABC vuông tại A, kẻ \(AH \bot BC(H \in BC)\) . Trên tia đối của tia HA ta lấy điểm M sao cho HM = HA.
a) Chứng minh rằng \(\Delta ABH = \Delta MBH\)
b) Gọi I là trung điểm của BC. Qua C kẻ đường thẳng vuông góc với AC, đường kẻ này cắt tia AI tại D. Chứng minh rằng AB = DC.
c) Chứng minh rằng \(\widehat {ACB} = \widehat {AMB}\)
d) Chứng minh rằng BC // DM.
Lời giải chi tiết
a)Xét tam giác AHB và MHB có:
HA = HM (giả thiết)
\(\widehat {AHB} = \widehat {MHB}( = {90^0})\)
BH là cạnh chung.
Dó đó: \(\Delta AHB = \Delta MHB(c.g.c).\)
b) Ta có: \(BA \bot AC\)(tam giác ABC vuông tại A) và \(DC \bot AC(gt)\)
\( \Rightarrow AB//CD \Rightarrow \widehat {ABI} = \widehat {DCI}\)
Xét tam giác ABI và DCI có:
\(\widehat {ABI} = \widehat {DCI}(cmt)\)
BI = CI (I là trung điểm của BC)
Và \(\widehat {AIB} = \widehat {DIC}\)(hai góc đối đỉnh)
Do đó: \(\Delta ABI = \Delta DCI(g.c.g)\)
Suy ra : AB = CD.
c) Ta có: \(\widehat {ACB} + \widehat {HAC} = {90^0}(\Delta AHC\)vuông tại H)
\(\eqalign{ & \widehat {BAH} + \widehat {HAC} = {90^0}(\widehat {BAC} = {90^0}) \cr & \Rightarrow \widehat {ACB} = \widehat {BAH} \cr} \)
Mà \(\widehat {BAH} = \widehat {BMH}(\Delta ABH = \Delta MBH)\) nên \(\widehat {ACB} = \widehat {AMB}\)
d) Cách 1:
Gọi O là giao điểm của BD và CM.
Xét tam giác MBC và DCB có:
BM = CD (=AB)
\(\widehat {MBC} = \widehat {DCB}( = \widehat {ABH})\)
BC là cạnh chung.
Do đó: \(\Delta MBC = \Delta DCB(c.g.c) \)
\(\Rightarrow \widehat {BCM} = \widehat {CBD} \)
\(\Rightarrow \widehat {BCM} = ({180^0} - \widehat {BOC}):2(1)\)
Xét tam giác BDM và CMD có:
\(BD = CM(\Delta MBC = \Delta DCB)\)
BM = CD
MD là cạnh chung.
Do đó: \(\Delta BDM = \Delta CMD(c.c.c) \)
\(\Rightarrow \widehat {BDM} = \widehat {CMD} \)
\(\Rightarrow \widehat {CMD} = ({180^0} - \widehat {MOD}):2(2)\)
Mà \(\widehat {BOC} = \widehat {MOD}(3)\) (đối đỉnh)
Từ (1), (2), (3) ta có: \(\widehat {BCM} = \widehat {CMD}\)
Mà góc BCM và CMD co le trong do đó: BC // DM.
Cách 2:
Gọi N là trung điểm của MD
Xét hai tam giác HAI và HMI có:
HA = HM (gt)
\(\widehat {AHI} = \widehat {MHI}( = {90^0})\)
IH là cạnh chung.
Do đó: \(\Delta HAI = \Delta HMI(c.g.c) \Rightarrow IA = IM,\widehat {HAI} = \widehat {HMI}.\)
Mà IA = ID \((\Delta ABI = \Delta DCI) \Rightarrow IM = ID\)
Xét tam giác IMN và IDN có:
IM = ID
IN là cạnh chung
MN = DN (N là trung điểm của MD)
Do đó: \(\Delta IMN = \Delta IDN(c.c.c) \)
\(\Rightarrow \widehat {IMN} = \widehat {IDN}.\)
Ta có:
\(\widehat {HAI} + \widehat {IDN} = \widehat {HMI} + \widehat {IMN} \)
\(\Rightarrow \widehat {MAD} + \widehat {ADM} = \widehat {AMD}\)
Tam giác AMD có: \(\widehat {MAD} + \widehat {ADM} + \widehat {AMD} = {180^0}.\)
Do đó: \(\widehat {AMD} + \widehat {AMD} = {180^0} \)
\(\Rightarrow 2\widehat {AMD} = {180^0} \Rightarrow \widehat {AMD} = {90^0} \Rightarrow AM \bot DM\)
Ta có: \(AM \bot BC;AM \bot DM.\) Vậy BC // DM.
dapandethi.vn
