Đề bài
Cho tam giác nhọn ABC. Trên tia đối của tia AB lấy điểm D sao AD = AB. Trên cạnh AC lấy điểm E sao cho \(AE = {1 \over 3}AC\) .
a) Chứng minh E là trọng tâm tam giác BCD.
b) Gọi M là trung điểm của DC. Chứng minh ba điểm B, M, E thẳng hàng.
Lời giải chi tiết
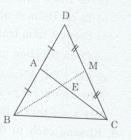
a) Xét ∆BCD có: CA là đường trung tuyến (AD = AB)
E trên đoạn thẳng CA
\(CE = {2 \over 3}CA\) (vì\(AE = {1 \over 3}AC\))
Nên E là trọng tâm của tam giác BCD.
b) ∆BDC có: BM là đường trung tuyến (M là trung điểm của DC)
E là trọng tâm (câu a)
Do đó BM đi qua E. Vậy B, M, E thẳng hàng.
dapandethi.vn
