Đề bài
Cho tam giác ABC vuông tại A. Lấy điểm H thuộc cạnh AB. Vẽ HM vuông góc với BC tại M. Tia MH cắt tia CA tại N. Chứng minh rằng CH vuông góc với NB.
Lời giải chi tiết
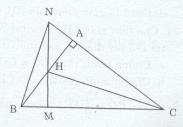
Xét ∆NBC có:
BA là đường cao \((BA \bot AC,N \in CA)\)
NM là đường cao \((HM \bot BC,N \in MH)\)
Và BA cắt NM tại H (gt)
Do đó H là trực tâm của ∆NBC
=> CH là đường cao của ∆NBC
Vậy \(CH \bot NB.\)
dapandethi.vn
