Đề bài
Cho góc xOy. Lấy các điểm A, B thuộc tia Ox sao cho OA < OB. Lấy C, D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC. Chứng minh rằng:
a) AD = BC
b) \(\Delta EAB = \Delta ECD\)
c) OE là tia phân giác góc xOy.
Lời giải chi tiết
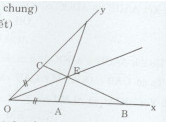
a)Xét tam giác OCB và OAD có:\(\eqalign{ & OC{\rm{ }} = {\rm{ }}OA{\rm{ }}\left( {gt} \right) \cr & \widehat {COB} = \widehat {AOD}(gocchung) \cr & OB = OD(gt) \cr} \)
Do đó: \(\Delta OCB = \Delta OAD(c.g.c) \Rightarrow BC = AC\)
b) Ta có:
\(\eqalign{ & *\Delta OCB = \Delta OAD \cr & \Rightarrow \widehat {ODA} = \widehat {OBC};\widehat {OCB} = \widehat {OAD} \cr} \)
*OC + CD = OD và OA + AB = OB
Mà OC = OA và OD = OB nên CD = AB.
*\(\widehat {OCE} + \widehat {ECD} = {180^0}\) (kề bù) và \(\widehat {OAE} + \widehat {EAB} = {180^0}\) (kề bù).
Mà \(\widehat {OCE} = \widehat {OAE}(cmt)\) nên \(\widehat {ECD} = \widehat {EAB}\)
Xét tam giác EAB và ECD có: \(\eqalign{ & \widehat {EAB} = \widehat {ECD}(cmt) \cr & AB = CD(cmt) \cr & \widehat {EBA} = \widehat {EDC}(\widehat {ODA} = \widehat {OBC}) \cr} \)
Do đó: \(\Delta EAB = \Delta ECD(g.c.g).\)
c)Ta có: \(\Delta EAB = \Delta ECD \Rightarrow EB = ED;\widehat {EBA} = \widehat {EDC}\)
Xét tam giác OEB và OED có: \(\eqalign{ & OB = OD(gt) \cr & \widehat {OBE} = \widehat {ODE}(cmt) \cr & EB = ED(cmt) \cr} \)
Do đó: \(\Delta OEB = \Delta OED(c.g.c) \Rightarrow \widehat {EOB} = \widehat {EOD}\)
Vậy OE là tia phân giác của góc xOy.
dapandethi.vn
