Bài 9 trang 55 SBT Hình học 12 Nâng cao

Đề bài

Chứng minh rằng nếu tứ diện ABCD có tính chất

AB+CD = AC+BD = AD+BC

Thì có mặt cầu tiếp xác với các cạnh của tứ diện ABCD.

Lời giải chi tiết

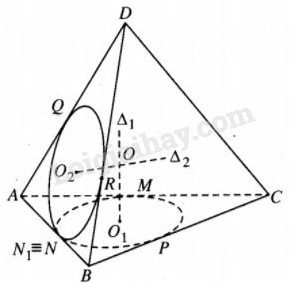
Gọi O₁ là tâm đường tròn nội tiếp tam giác ABC và các điểm tiếp xúc của đường tròn đó với các cạnh M, N, P.

Gọi \({\Delta _1}\) là trục của đường tròn này thì \({\Delta _1}\) chứa tâm của các mặt cầu tiếp xúc với ba cạnh AB, BC, CA.

Tương tự, nếu gọi \({\Delta _2}\) là trục của đường tròn nội tiếp tam giác ABD thì \({\Delta _2}\) chứa tâm của các mặt cầu tiếp xúc với ba cạnh của tam giác ABD .

Kí hiệu điểm tiếp xúc của ba cạnh ấy với đường tròn nội tiếp \(\Delta ABD\)  là N₁, Q, R (N₁ thuộc AB).

Khi ấy, vì

\(AN = {{AB + AC - BC} \over 2},A{N_1} = {{AB + AD - BD} \over 2}\)

Mà AC+BD = AD+BC nên AN = AN₁, từ đó \(N \equiv {N_1}.\)

Suy ra \(AB \bot mp({O_1}N{O_2}).\)

Mặt khác, \({\Delta _1} \bot AB\) và cắt mp(ABC) tại \({O_1},{\Delta _2}\) vuông góc với AB và cắt mp(ABD) tại O₂ nên \({\Delta _1},{\Delta _2}\) cùng nằm trong mp(\({O_1}N{O_2}\)).

Từ đó \({\Delta _1}\) cắt \({\Delta _2}\) tại O, đó là điểm cách đều năm cạnh AB, AC, BC, AD, BD của tứ diện ABCD hay

OM = ON = OP = OQ = OR.                 (1)

Hoàn toàn tương tự như trên ta cũng có \({\Delta _2}\) cắt \({\Delta _3}\) (\({\Delta _3}\) là trục của đường tròn nội tiếp tam giác ACD) tại O’ và

O’M = O’N = O’Q = O’R = O’S             (2)

(S là điểm tiếp xúc của cạnh CD và đường tròn nội tiếp \(\Delta ACD\)).

Từ (1) và (2) ta có O, O’ cùng là tâm của mặt cầu đi qua bốn điểm M, N, Q, R mà M, N, Q, R không đồng phẳng, vậy \(O \equiv O'.\)

Đó là tâm mặt cầu tiếp xúc với sáu cạnh của tứ diện, bán kính mặt cầu đó là ON.

dapandethi.vn