Đề bài
Cho đường tròn đường kính AB = 2R nằm trong mặt phẳng (P). Gọi O1 là điểm đối xứng với O qua A. Lấy điểm S sao cho SO1 vuông góc với (P) và SO1 = 2R. Tính thể tích của khối cầu đi qua đường tròn đã cho và điểm S.
Lời giải chi tiết
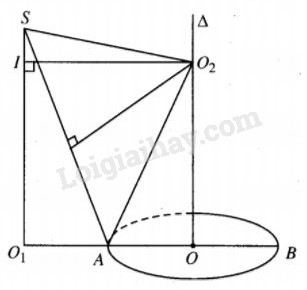
Gọi \(\Delta \) là trục của đường tròn đã cho thì \(\Delta // S{O_1}\).
Trong \(mp(S{O_1},\Delta ),\) đường trung trực của SA cắt \(\Delta \) tại O2 thì O2 là tâm mặt cầu đi qua đường tròn đã cho và điểm S, bán kính mặt cầu này bằng \({O_2}A = {O_2}S\).
Xét các tam giác vuông \({O_2}AO\) và \({O_2}{\rm{IS}}\) ( ở đó \({O_2}I// A{O_1})\), ta có
\(\eqalign{ & {O_2}{S^2} = 4{R^2} + {(2R - O{O_2})^2} \cr & {O_2}A^2 = {R^2} + OO_2^2. \cr} \)
Từ đó
\(4{R^2} + {(2R - O{O_2})^2} = {R^2} + OO_2^2,\) suy ra \(O{O_2} = {{7R} \over 4}\).
Vậy bán kính mặt cầu là \(\sqrt {{R^2} + {{49} \over {16}}{R^2}} = {{R\sqrt {65} } \over 4}\)
Và thể tích khối cầu phải tìm là \({{65} \over {48}}\sqrt {65} \pi {R^3}.\)
dapandethi.vn
