Cho tam giác ABC vuông ở A, BC = 2a, \(\widehat {ACB}\) =300. Xét hai tia Bx, Cy cùng hướng và cùng vuông góc với mp(ABC)
LG 1
Xác định vị trí điểm B1 trên Bx sao cho mặt cầu đường kính BB1 tiếp xúc với Cy.
Xác định điểm C1 trên Cy sao cho mặt cầu đường kính AC1 tiếp xúc với Bx.
Lời giải chi tiết:
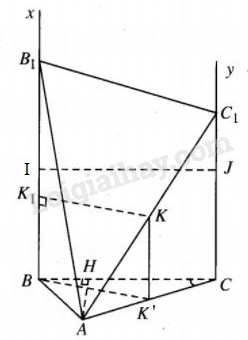
Gọi I là trung điểm của BB1 thì mặt cầu đường kính BB1 tiếp xúc với Cy tại J khi và chỉ khi \(IJ = {1 \over 2}B{B_1}\).
Mặt khác, dễ thấy IJ = BC = 2a.
Vậy BB1 = 4a. Hệ thức này xác định vị trí điểm B1.
\( \bullet \) Gọi K là trung điểm của AC1 thì mặt cầu đường kính AC1 tiếp xúc với Bx khi và chỉ khi khoảng cách từ điểm K đến Bx bằng \({1 \over 2}A{C_1}\), tức là \(K{K_1} = {1 \over 2}A{C_1}\) hay \(BK' = {1 \over 2}A{C_1}\), trong đó K’ là trung điểm của AC.
Dễ thấy AB = a, \(AC = a\sqrt 3 \), từ đó
\(BK{'^2} = {a^2} + {\left( {{{a\sqrt 3 } \over 2}} \right)^2} = {{7{a^2}} \over 4} \Rightarrow BK' = {{a\sqrt 7 } \over 2}.\)
Như vậy,mặt cầu đường kính AC1 tiếp xúc với Bx khi và chỉ khi \(A{C_1} = a\sqrt 7 \), từ đó \(CC_1^2 = 7{a^2} - 3{a^2} = 4{a^2}\), tức là \(C{C_1} = 2a\).
Hệ thức này xác định vị trí điểm C1. (Khi đó \(J \equiv {C_1}).\)
LG 2
Với các điểm B1, C1 tìm được ở trên, hỏi đa diện ABCC1B1 có mặt cầu ngoại tiếp không ? Hãy tính thể tích của khối đa diện đó.
Lời giải chi tiết:
\( \bullet \) Khi BB1 = 4a, CC1 = 2a thì \(B{B_1}{C_1}C\) là hình thang vuông tại B, C với hai đáy có độ dài khác nhau nên \(B{B_1}{C_1}C\) không có đường tròn ngoại tiếp. Vậy đa diện \(ABC{C_1}{B_1}\) không có mặt cầu ngoại tiếp.
Dễ thấy A.BCC1B1 là hình chóp đỉnh A, đáy là BCC1B1 và mp(ABC) vuông góc với mp(BCC1B1). Từ đó
\({V_{A.BC{C_1}{B_1}}} = {1 \over 3}.{1 \over 2}(B{B_1} + C{C_1}).BC.AH\)
(AH là đường cao của tam giác vuông ABC)
Hay \({V_{A.BC{C_1}{B_1}}} = {1 \over 6}(4a + 2a).AB.AC\)
\(= {1 \over 6}.6a.a.a\sqrt 3 = {a^3}\sqrt 3 .\)
dapandethi.vn
