Cho mặt cầu tâm O bán kính R và A là điểm cố định thuộc mặt cầu. Ba tia \(A{t_1},A{t_2},A{t_3}\) thay đổi, đôi một vuông góc với nhau và cắt mặt cầu tại các điểm B, C, D.
LG 1
Chứng minh rằng hình hộp dựng trên ba cạnh AB, AC, AD có một đường chéo cố định và mp(BCD) luôn luôn đi qua một điểm cố định.
Lời giải chi tiết:
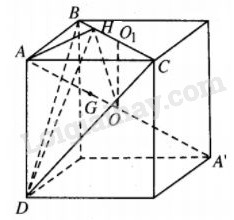
Dễ thấy các đỉnh của hình hộp chữ nhật dựng trên ba cạnh AB, AC, AD cũng thuộc mặt cầu đã cho.
Khi ấy tâm O của mặt cầu là trung điểm của đường chéo AA’ của hình hộp, tức là hình hộp nêu trên có một đường chéo cố định là AA’.
Mặt khác AA’ cắt mp(BCD) tại trọng tâm G của tam giác BCD và \(\overrightarrow {AG} = {1 \over 3}\overrightarrow {AA'} \).
Vậy mp(BCD) luôn luôn đi qua điểm cố định G nói trên.
LG 2
Chứng minh rằng hình chiếu H của điểm D trên đường thẳng BC thuộc một mặt cầu cố định.
Lời giải chi tiết:
Vì \(DH \bot BC,DA \bot mp(ABC)\) nên \(AH \bot BC\).
Gọi O1 là trung điểm của BC thì \({\rm{O}}{{\rm{O}}_1} \bot (BCA) \Rightarrow O{O_1} \bot AH,\) từ đó \(AH \bot HO.\)
Điều này khẳng định điểm H thuộc mặt cầu đường kính AO, mặt cầu này cố định vì A, O cố định.
dapandethi.vn
