Đề bài
Cho điểm \(D\) nằm trong tam giác \(ABC\) sao cho \(\widehat {DAB} = \widehat {DBC} = \widehat {DCA} = \varphi .\) Chứng minh rằng:
a) \({\sin ^3}\varphi = \sin (A - \varphi )\)\(.\sin (B - \varphi ).\sin (C - \varphi ).\)
b) \(\cot \varphi = \cot A + \cot B + \cot C.\)
Lời giải chi tiết
(h.75).
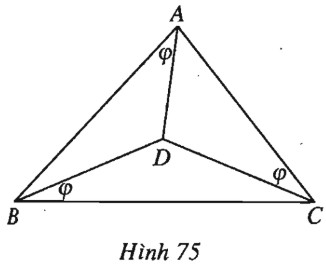
a) Theo định lí sin, trong tam giác \(ABD\) ta có
\(\dfrac{{DB}}{{\sin \varphi }} = \dfrac{{AD}}{{\sin (B - \varphi )}}\) , (1)
trong tam giác BCD có
\(\dfrac{{CD}}{{\sin \varphi }} = \dfrac{{BD}}{{\sin (C - \varphi )}}\), (2)
trong tam giác \(ACD\) có
\(\dfrac{{AD}}{{\sin \varphi }} = \dfrac{{CD}}{{\sin (A - \varphi )}}\).
Từ đó ta có
\(\dfrac{{AD.BD.CD}}{{{{\sin }^3}\varphi }}\)
\(= \dfrac{{AD.BD.CD}}{{\sin (A - \varphi )\sin (B - \varphi )\sin (C - \varphi )}}\).
Suy ra đẳng thức cần chứng minh.
b) Áp dụng định lí cosin vào tam giác \(DAB\) ta có
\(B{D^2}\)\( = A{B^2} + A{D^2} - 2.AB.AD.\cos \varphi. \)
Mặt khác, \(\dfrac{1}{2}AB.AD.\sin \varphi = {S_{ABD}}\) .
Từ đó suy ra \(B{D^2} = A{B^2} + A{D^2} - 4{S_{ABD}}.\cot \varphi \).
Tương tự ta cũng có \(C{D^2} = B{C^2} + B{D^2} - 4{S_{DBC}}.\cot \varphi ;\) \( A{D^2} = A{C^2} + C{D^2} - 4{S_{DCA}}.\cot \varphi. \)
Cộng theo vế rồi biến đổi, chú ý rằng tổng diện tích ba tam giác nhỏ bằng diện tích \(S\) của tam giác \(ABC\), ta được
\(\cot \varphi = \dfrac{{{a^2} + {b^2} + {c^2}}}{{4S}}\) \( = \dfrac{{{a^2} + {b^2} + {c^2}}}{{abc}}R.\)
Theo bài 58 chương II, \(\cot A + \cot B + \cot C\) \( = \dfrac{{{a^2} + {b^2} + {c^2}}}{{abc}}R.\)
Từ đó suy ra đẳng thức cần chứng minh.
dapandethi.vn
