Biết rằng tam giác \(ABC\) có \(AB=10, AC=4\) và \(\widehat A = {60^0}\).
LG a
Tính chu vi của tam giác.
Lời giải chi tiết:
Ta đi tìm độ dài cạnh \(BC\).
Áp dụng định lí cosin, ta có
\(B{C^2} = {10^2} + {4^2} - 2.4.10.\cos {60^0} = 76\)
Suy ra \(BC \approx 8,72\).
Chu vi tam giác \(2p \approx 10 + 4 + 8,72 \approx 22,72\).
LG b
Tính \(\tan C.\)
Lời giải chi tiết:
(h.73).
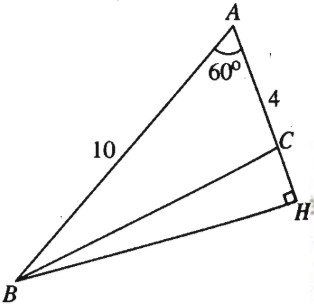
Kẻ đường cao \(BH\) ta có \(AH = AB. \cos {60^0} = 5\), suy ra \(HC=5-4=1.\)
\(BH = AB.\sin {60^0} = 5\sqrt 3 ,\) \( \tan C = - \tan \widehat {BCH} = - \dfrac{{HB}}{{HC}}\)\( = - 5\sqrt 3 \).
LG c
Lấy điểm \(D\) trên tia đối của tia \(AB\) sao cho \(AD=6\) và điểm \(E\) trên tia \(AC\) sao cho \(AE=x\). Tìm \(x\) để \(BE\) là tiếp tuyến của đường tròn \((ADE)\) (\((ADE)\) là đường tròn ngoại tiếp tam giác \(ADE\)).
Lời giải chi tiết:
(h.74).
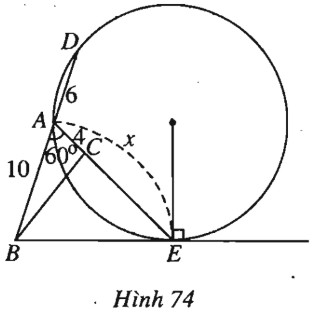
Để \(BE\) là tiếp tuyến của đường tròn \((ADE)\) phải có \(B{E^2} = BA.BD = 10(10 + 6) = 160\).
Ta có \(AE = x\), áp dụng định lí cosin cho tam giác \(ABE\) :
\(B{E^2} = {x^2} + 100 - 10x\).
Từ đó có phương trình: \({x^2} - 10x + 100 - 160\) hay \({x^2} - 10 - 60 = 0\), phương trình này có một nghiệm dương là \(x = 5 + \sqrt {85} \). Vậy điểm \(E\) cần tìm là điểm trên tia \(AC\) và cách \(A\) một khoảng bằng \(5 + \sqrt {85} \).
dapandethi.vn
