Đề bài
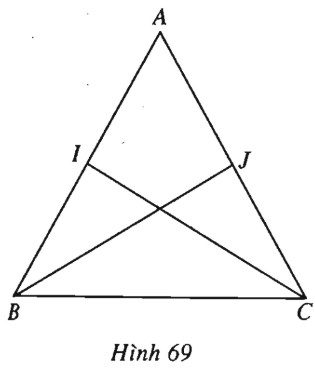
Cho tam giác đều \(ABC\) có \(I, J\) lần lượt là trung điểm của \(AB, AC\). Tìm \(\cos (\overrightarrow {AB} ,\overrightarrow {AC} ), \cos (\overrightarrow {AB} ,\overrightarrow {BC} ), \) \( \cos (\overrightarrow {BJ} ,\overrightarrow {BC} ), \cos (\overrightarrow {AB} ,\overrightarrow {BJ} ),\) \( \cos (\overrightarrow {BJ} ,\overrightarrow {CI} ). \)
Lời giải chi tiết
(h.69).
\(\begin{array}{l}\cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \cos {60^0} = \dfrac{1}{2}.\\\cos \left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) = \cos {120^0} = - \dfrac{1}{2}.\\\cos \left( {\overrightarrow {BJ} ,\overrightarrow {BC} } \right) = \cos {30^0} = \dfrac{{\sqrt 3 }}{2}.\\\cos \left( {\overrightarrow {AB} ,\overrightarrow {BJ} } \right) = \cos {150^0} = - \dfrac{{\sqrt 3 }}{2}.\\\cos \left( {\overrightarrow {BJ} ,\overrightarrow {CI} } \right) = \cos {120^0} = - \dfrac{1}{2}.\end{array}\)
dapandethi.vn
