Cho hàm số \(y = 0,1{x^2}\)
LG a
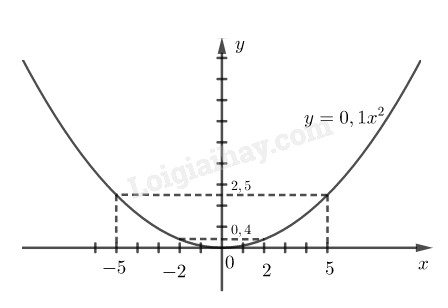
Vẽ đồ thị của hàm số.
Phương pháp giải:
Lấy một số điểm thuộc đồ thị hàm số bằng cách thay một số giá trị của \(x\) để tìm giá trị của \(y\), rồi từ đó vẽ đồ thị.
Lời giải chi tiết:
Vẽ đồ thị hàm số \(y = 0,1{x^2}\)
|
\(x\) |
\(-5\) |
\(-2\) |
\(0\) |
\(2\) |
\(5\) |
| \(y = 0,1{x^2}\) |
\(2,5\) |
\(0,4\) |
\(0\) |
\(0,4\) |
\(2,5\) |
LG b
Các điểm sau có thuộc đồ thị hay không: \(A(3; 0,9),\)\( B(-5; 2,5),\)\( C(-10, 1)?\)
Phương pháp giải:
Thay các giá trị \(x,y\) vào hàm số nếu thỏa mãn thì điểm đó thuộc đồ thị, nếu không thỏa mãn thì điểm đó không thuộc đồ thị.
Lời giải chi tiết:
Thay hoành độ điểm \(A\) vào phương trình hàm số:
\(y = 0,{1.3^2} = 0,9 = {y_A}\)
Vậy điểm \(A (3; 0,9)\) thuộc đồ thị hàm số.
Thay hoành độ điểm \(B\) vào phương trình hàm số:
\(y = 0,1{\left( { - 5} \right)^2} = 0,1.25 = 2,5 = {y_B}\)
Vậy điểm \(B (-5; 2,5)\) thuộc đồ thị hàm số.
Thay hoành độ điểm \(C\) vào phương trình hàm số:
\(y = 0,1{\left( { - 10} \right)^2} = 0,1.100 = 10 \ne {y_C}\).
Vậy điểm \(C (-10; 1)\) không thuộc đồ thị hàm số.
dapandethi.vn
