Cho hai hàm số \(y = 0,2{x^2}\) và \(y = x\)
LG a
Vẽ hai đồ thị của những hàm số này trên cùng một mặt phẳng tọa độ.
Phương pháp giải:
Lấy một số điểm thuộc đồ thị hàm số, rồi từ đó vẽ đồ thị.
Lời giải chi tiết:
Vẽ đồ thị hàm số \(y = 0,2{x^2}\)
|
\(x\) |
\(-5\) |
\(-2\) |
\(0\) |
\(2\) |
\(5\) |
| \(y = 0,2{x^2}\) |
\(5\) |
\(0,8\) |
\(0\) |
\(0,8\) |
\(5\) |
Vẽ đồ thị hàm số \(y = x\).
Cho \(x=0\Rightarrow y = 0\)
Cho \(x = 5 \Rightarrow y = 5.\)
Đồ thị hàm số \(y = x\) là đường thẳng đi qua hai điểm \(O(0;0\) và \(M(5; 5)\)
Vẽ hình:
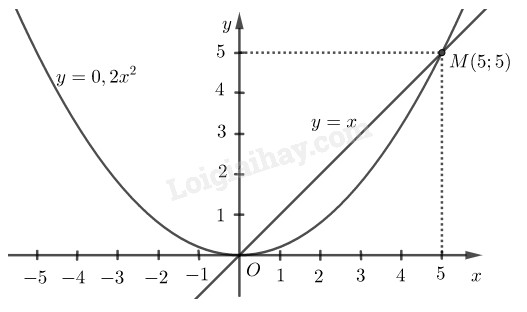
LG b
Tìm tọa độ của các giao điểm của hai đồ thị.
Phương pháp giải:
Để tìm tọa độ giao điểm của hai đồ thị, ta có phương trình hoành độ giao điểm, rồi từ đó tìm được \(x, y.\)
Lời giải chi tiết:
Phương trình hoành độ giao điểm của hai đồ thị hàm số là \(0,2x^2=x \) \(\Leftrightarrow 0,2x^2-x=0\)\(\Leftrightarrow x(0,2x-1)=0\)
\( \Leftrightarrow \left[ \begin{array}{l}
x = 0\\
0,2x = 1
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
x = 0 \Rightarrow y = 0\\
x = 5 \Rightarrow y = 5
\end{array} \right.\)
Vậy tọa độ giao điểm của hai đồ thị đó là \((0;0)\) và \((5;5).\)
dapandethi.vn
