Đề bài
Nghiệm của bất phương trình \(\dfrac{{{x^2} + x - 3}}{{{x^2} - 4}} \ge 1\) là
A. \( - 2 < x \le 1;x > 2\)
B. \( - 2 < x \le 1\);\(x \ge 2\)
C. \(x \le - 2; - 1 \le x \le 2\)
D. \(x \le - 2\);\( - 1 \le x < 2\)
Phương pháp giải - Xem chi tiết
Cách 1: - Đặt điều kiện
- Chuyển vế đổi dấu , cho \(f(x) = 0\) tìm các giá trị đặc biệt
- Lập bảng xét dấu và kết luận nghiệm
Cách 2: Xét các đáp án.
Lời giải chi tiết
Điều kiện \({x^2} - 4 \ne 0\)\( \Leftrightarrow x \ne \pm 2\)
\(\dfrac{{{x^2} + x - 3}}{{{x^2} - 4}} \ge 1\)\( \Leftrightarrow \dfrac{{{x^2} + x - 3}}{{{x^2} - 4}} - 1 \ge 0\)
\( \Leftrightarrow \dfrac{{x + 1}}{{(x - 2)(x + 2)}} \ge 0\)
\(f(x) = 0\)\( \Leftrightarrow \dfrac{{x + 1}}{{(x - 2)(x + 2)}} = 0\)\( \Leftrightarrow x + 1 = 0\)\( \Leftrightarrow x = - 1\)
Ta có bảng xét dấu
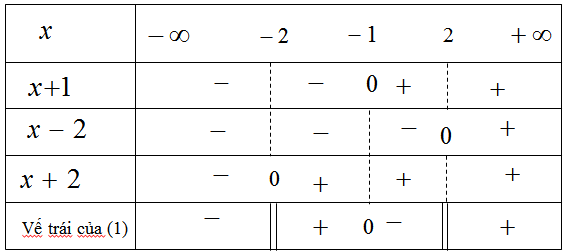
Nhìn vào bảng xét dấu ta thấy
\(f(x) \ge 0\) khi \( - 2 < x \le - 1,x > 2\)
Đáp án A.
dapandethi.vn
