Đề bài
Giải bất phương trình sau
\(\dfrac{3}{{2 - x}} < 1\)
Phương pháp giải - Xem chi tiết
- Đặt điều kiện
- Chuyển vế đổi dấu , cho \(f(x) = 0\) tìm các giá trị đặc biệt
- Lập bảng xét dấu và kết luận nghiệm
Lời giải chi tiết
Điều kiện \(2 - x \ne 0\)\( \Leftrightarrow x \ne 2\)
\(\dfrac{3}{{2 - x}} < 1\)\( \Leftrightarrow \dfrac{3}{{2 - x}} - 1 < 0\)\( \Leftrightarrow \dfrac{{3 - 2 + x}}{{2 - x}} < 0\)\( \Leftrightarrow \dfrac{{x + 1}}{{2 - x}} < 0 (1)\)
\( \Leftrightarrow \dfrac{{x + 1}}{{2 - x}} = 0\)\( \Leftrightarrow x + 1 = 0\)\( \Leftrightarrow x = - 1\)
Bảng xét dấu vế trái của (1)
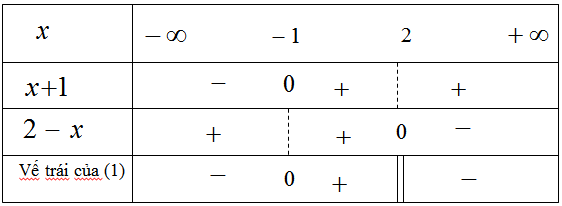
Từ bảng xét dấu ta thấy
\(f(x) < 0\) khi \(x \in ( - \infty ; - 1)\) hoặc \(x \in (2; + \infty )\)
Vậy tập nghiệm của bất phương trình là \(x < - 1,x > 2\)
dapandethi.vn
