Đề bài
Xét dấu biểu thức sau:
\(f(x) = \dfrac{{2x + 1}}{{(x - 1)(x + 2)}}\).
Phương pháp giải - Xem chi tiết
- Đặt điều kiện cho f(x)
- Tìm các giá trị làm cho \(f(x) = 0\)
- Kẻ bảng xét dấu
- Đưa ra kết luận dựa vào bảng xét dấu
Lời giải chi tiết
Điều kiện: \((x-1)(x+2) \ne 0\)\( \Leftrightarrow x \ne 1;x \ne - 2\)
\(f(x) = 0\) \( \Leftrightarrow \dfrac{{2x + 1}}{{(x - 1)(x + 2)}} = 0\)\( \Leftrightarrow 2x + 1 = 0\)\( \Leftrightarrow x = - \dfrac{1}{2}\)
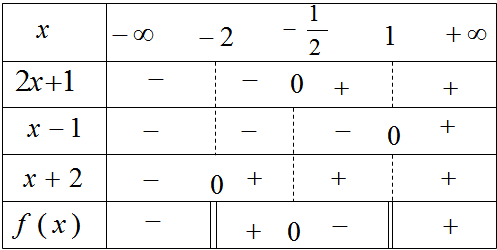
Từ bảng xét dấu ta thấy:
\(f(x) > 0\) khi \(x \in ( - 2; - \dfrac{1}{2})\) hoặc \(x \in (1; + \infty )\)
\(f(x) < 0\) khi \(x \in ( - \infty ; - 2)\) hoặc \(x \in ( - \dfrac{1}{2};1)\)
\(f(x) = 0\) khi \(x = - \dfrac{1}{2}\)
\(f(x)\) không xác định khi \(x = - 2\) hoặc \(x = 1\).
dapandethi.vn
