Đề bài
Tính diện tích toàn phần của:
a) Hình chóp tứ giác đều, biết cạnh đáy \(a = 5cm\), cạnh bên \(b = 5cm,\;\sqrt{18,75}\approx 4,33 \)
b) Hình chóp lục giác đều, biết cạnh đáy \(a = 6cm\), cạnh bên \(b = 10cm,\; \sqrt{3}\approx 1,73; \;\sqrt{91}\approx 9,54\)
Phương pháp giải - Xem chi tiết
Áp dụng các công thức :
\(S_{tp} = S_{xq} +S{đ}\)
\(S_{xq} = p.d \), trong đó \(p \) là nửa chu vi đáy, \( d\) là trung đoạn của hình chóp.
Lời giải chi tiết
a)
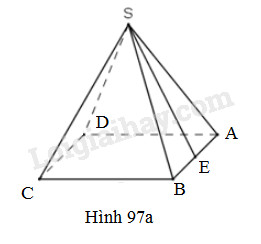
Gọi hình chóp tứ giác đều trong câu a) (h.97a) là \(S.ABCD\), trong đó SE là trung đoạn của hình chóp. Ta có: \(AB=5cm,SA=5cm,\) \(AE=\dfrac{1}2AB=2,5cm.\)
- Xét tam giác vuông SEA, ta có:
\(SE = \sqrt{SA^{2} -EA^{2}}\)
\(= \sqrt{5^{2} -2,5^{2}}= \sqrt{18,75}\approx 4,33 (cm) \)
- Diện tích xung quanh:
\(S_{xq} = p.d \approx \dfrac{1}{2}. 5.4.4,33 = 43,3 (cm^2) \)
- Diện tích đáy:
\(S_{đáy} = AB^2 = 5^2 =25(cm^2) \)
- Diện tích toàn phần:
\( S_{tp} = S_{xq}+ S_{đáy} \approx 43,3 + 25 = 68,3 \) \((cm^2)\)
b)
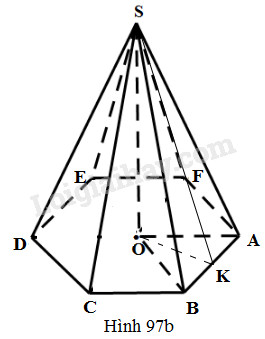
Gọi hình chóp lục giác đều trong câu b) (h.97b) là \(S.ABCDEF\), trong đó \(SK\) là trung đoạn của hình chóp, \(SO\) là đường cao. Ta có: \(AB=6cm,SA=10cm,\) \(AK=\dfrac{1}2 AB=3cm\).
- Trung đoạn của hình chóp là :
\(SK = \sqrt{SA^{2} -AK^{2}} = \sqrt{10^{2} -3^{2}} \) \(= \sqrt{91}\approx 9,54 (cm) \)
- Diện tích xung quanh:
\(S_{xq} =\dfrac{1}{2}. 6AB.SK\approx \dfrac{1}{2}. 6.6.9,54 = 171,72\) \( (cm^2) \)
- Diện tích tam giác \(OAB\):
\({S_{OAB}} = \dfrac{{A{B^2}\sqrt 3 }}{4} = \dfrac{{{6^2}\sqrt 3 }}{4} \)\(= 9\sqrt 3 \approx 9.1,73 = 15,57\left( {c{m^2}} \right)\)
- Diện tích đáy hình chóp:
\(S_{đáy} =6. {S_{OAB}}\approx 6.15,57 = 93,42(cm^2) \)
- Diện tích toàn phần hình chóp:
\( S_{tp} = S_{xq}+ S_{đáy} \approx 171,72 + 93,42 \) \(= 265,14 (cm^2)\)
dapandethi.vn
