Đề bài
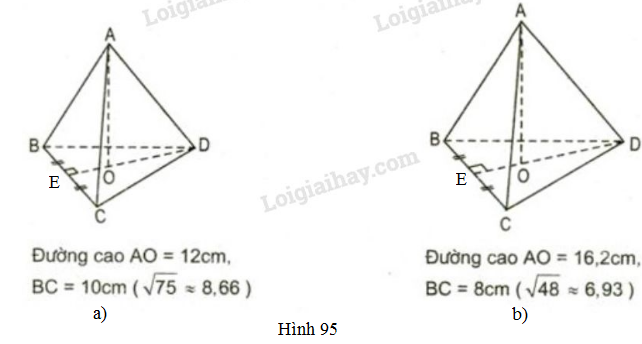
Tính thể tích của mỗi hình chóp đều dưới đây (h.95).
Phương pháp giải - Xem chi tiết
Tính thể tích hình chóp theo công thức: \(V = \dfrac{1}{3} .S.h\), trong đó \(S\) là diện tích đáy, \(h\) là chiều cao.
Lời giải chi tiết
a) Theo đề bài, \(A.BCD\) là hình chóp tam giác đều, đáy BCD là tam giác đều có cạnh \(BC=10cm\), đường cao hình chóp \(AO=12cm\). Trên hình vẽ, ta có \(DE\) là đường cao của \(\Delta BCD \Rightarrow EB=EC=\dfrac{BC}{2}\)
- Tam giác BED vuông tại E, theo định lý Py-ta-go ta có:
\(DE = \sqrt {B{D^2} - B{E^2}} = \sqrt {{{10}^2} - {5^2}}\)\( = \sqrt {75} \approx 8,66\left( {cm} \right)\)
- Diện tích tam giác BDC là:
\(S_{BCD}= \dfrac{1}{2}. BC. DE = \dfrac{1}{2}. 10. \sqrt {75} \approx 43,3 \) \((cm^2) \)
Thể tích hình chóp \(A.BDC\) là:
\( V= \dfrac{1}{3} .S_{BCD}.AO = \dfrac{1}{3} .43,3 .12 =173,2 \) \((cm^3)\)
b) Hoàn toàn tương tự như câu a), ta có
\(DE = \sqrt {B{D^2} - B{E^2}} = \sqrt {{{8}^2} - {4^2}}\)\( = \sqrt {48} \approx 6,93\left( {cm} \right)\)
\(S_{BCD}= \dfrac{1}{2}. BC. DE = \dfrac{1}{2}. 8. 6,93 =27,72 \) \((cm^2) \)
\( V= \dfrac{1}{3} .S_{BCD}.AO = \dfrac{1}{3} .27,72 .16,2 \)\(\,\approx 149,69\) \( (cm^3)\)
dapandethi.vn