Video hướng dẫn giải

Lựa chọn câu để xem lời giải nhanh hơn

Rút gọn các biểu thức sau:

LG a

\(\;{\left( {a + b} \right)^2} - {\left( {a - b} \right)^2}\);

Phương pháp giải:

Áp dụng các hằng đẳng thức đáng nhớ để khai triển phá ngoặc, sau đó rút gọn các đơn thức đồng dạng.

\(1)\,{\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\)

\(2)\,{\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\)

\(3)\,{A^2} - {B^2} = \left( {A + B} \right)\left( {A - B} \right)\)

Lời giải chi tiết:

\(\eqalign{
& \,\,{\left( {a + b} \right)^2} - {\left( {a - b} \right)^2} \cr 
& = ({a^2} + 2ab + {b^2}) - ({a^2} - 2ab + {b^2}) \cr 
& = {a^2} + 2ab + {b^2} - {a^2} + 2ab - {b^2} \cr 
& = \left( {{a^2} - {a^2}} \right) + 2ab + 2ab + \left( {{b^2} - {b^2}} \right) \cr 
& = 4ab \cr} \)

Cách 2:

\(\eqalign{
& {\left( {a + b} \right)^2} - {\left( {a - b} \right)^2} \cr 
& = \left[ {\left( {a + b} \right) + \left( {a - b} \right)} \right].\left[ {\left( {a + b} \right) - \left( {a - b} \right)} \right] \cr 
& = \left( {a + b + a - b} \right)\left( {a + b - {\rm{ }}a + b} \right) \cr 
& = 2a.2b = 4ab \cr} \)

LG b

\(\,\,{\left( {a + b} \right)^3} - {\left( {a - b} \right)^3} - 2{b^{3}}\)

Phương pháp giải:

Áp dụng các hằng đẳng thức đáng nhớ để khai triển phá ngoặc, sau đó rút gọn các đơn thức đồng dạng.

\(4)\,{\left( {A + B} \right)^3} = {A^3} + 3{A^2}B + 3A{B^2} + {B^3}\)

\(5)\,{\left( {A - B} \right)^3} = {A^3} - 3{A^2}B + 3A{B^2} - {B^3}\) 

\(7)\,{A^3} - {B^3} = \left( {A - B} \right)({A^2} + AB + {B^2})\)

Lời giải chi tiết:

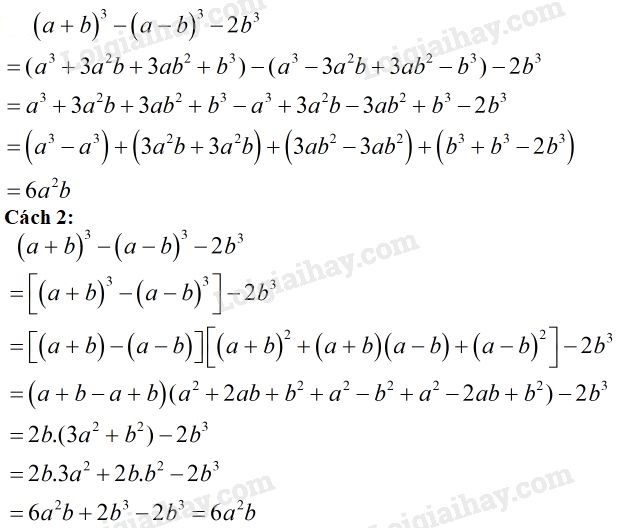
LG c

\(\;{\left( {x + y + z} \right)^2} - 2\left( {x + y + z} \right)\left( {x + y} \right) + {\left( {x + y} \right)^2}\)

Phương pháp giải:

Áp dụng các hằng đẳng thức đáng nhớ để khai triển phá ngoặc, sau đó rút gọn các đơn thức đồng dạng.

\(2)\,{\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\) 

Hoặc áp dụng kết quả:

\({\left( {x + y + z} \right)^2} = {x^2} + {y^2} + {z^2} + 2xy + 2yz + 2xz\)

Lời giải chi tiết:

Đặt \(A=x+y+z; B=x+y\)

Ta có:

\(\eqalign{
& {\left( {x + y + z} \right)^2} - 2\left( {x + y + z} \right)\left( {x + y} \right) + {\left( {x + y} \right)^2} \cr 
& = {A^2} - 2AB + {B^2} = {\left( {A - B} \right)^2} \cr 
& = {\left[ {\left( {x + y + z} \right) - \left( {x + y} \right)} \right]^2} \cr 
& = {\left( {x + y + z - x - y} \right)^2} = {z^2} \cr} \)

Cách 2:

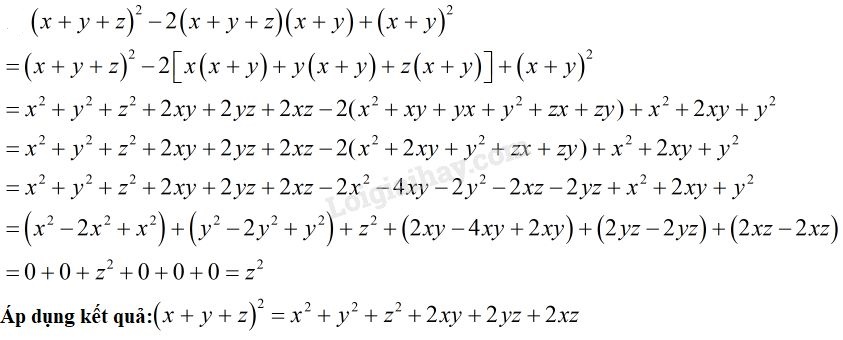
dapandethi.vn