Video hướng dẫn giải
Rút gọn các biểu thức sau:
LG a
\(\,\,\left( {x + 3} \right)({x^2} - 3x + 9) - (54 + {x^3})\)
Phương pháp giải:
Áp dụng: Hằng đẳng thức tổng hai lập phương, quy tắc phá dấu ngoặc.
\({A^3} + {B^3} = \left( {A + B} \right)({A^2} - AB + {B^2})\)
Lời giải chi tiết:
\(\eqalign{
& {\kern 1pt} {\kern 1pt} \left( {x + 3} \right)({x^2} - 3x + 9) - (54 + {x^3}) \cr
& = \left( {x + 3} \right)({x^2} - x.3 + {3^2}) - (54 + {x^3}) \cr
& = {x^3} + {3^3} - (54 + {x^3}) \cr
& = {x^3} + 27 - 54 - {x^3} \cr
& = \left( {{x^3} - {x^3}} \right) + \left( {27 - 54} \right) \cr
& = - 27 \cr} \)
LG b
\(\left( {2x + y} \right)(4{x^2} - 2xy + {y^2}) - \left( {2x - y} \right)(4{x^2} + 2xy + {y^2})\)
Phương pháp giải:
Áp dụng: Hằng đẳng thức tổng hai lập phương, hiệu hai lập phương, quy tắc phá dấu ngoặc.
\({A^3} + {B^3} = \left( {A + B} \right)({A^2} - AB + {B^2})\)
\({A^3} - {B^3} = \left( {A - B} \right)({A^2} + AB + {B^2})\)
Lời giải chi tiết:
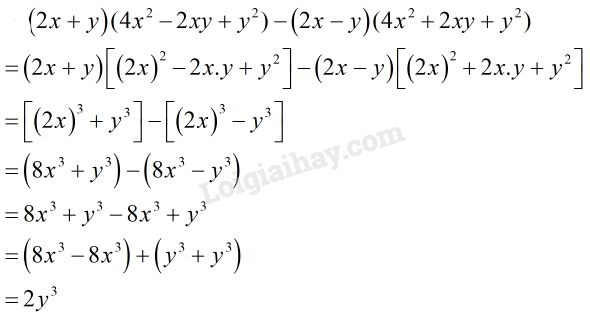
dapandethi.vn
