Chứng minh các tính chất sau đây có tích có hướng :
LG a
\(\eqalign{\left[ {\overrightarrow a ,\overrightarrow b } \right] = - \left[ { \overrightarrow b ,\overrightarrow a } \right]\cr} \)
Lời giải chi tiết:
Giả sử \(\overrightarrow a = ({x_1};{y_1};{z_1}),\overrightarrow b = ({x_2};{y_2};{z_2}),\overrightarrow c = ({x_3};{y_3};{z_3})\)
\(\eqalign{ &\left[ {\overrightarrow a ,\overrightarrow b } \right] = \left( {\left| \matrix{ {y_1} \hfill \cr {y_2} \hfill \cr} \right.\left. \matrix{ {z_1} \hfill \cr {z_2} \hfill \cr} \right|;\left| \matrix{ {z_1} \hfill \cr {z_2} \hfill \cr} \right.\left. \matrix{ {x_1} \hfill \cr {x_2} \hfill \cr} \right|;\left| \matrix{ {x_1} \hfill \cr {x_2} \hfill \cr} \right.\left. \matrix{ {y_1} \hfill \cr {y_2} \hfill \cr} \right|} \right) \cr & = ({y_1}{z_2} - {y_2}{z_1};{z_1}{x_2} - {z_2}{x_1};{x_1}{y_2} - {x_2}{y_1}) \cr & = - ({y_2}{z_1} - {y_1}{z_2};{z_2}{x_1} - {z_1}{x_2};{x_2}{y_1} - {x_1}{y_2}) \cr & = - \left( {\left| \matrix{ {y_2} \hfill \cr {y_1} \hfill \cr} \right.\left. \matrix{ {z_2} \hfill \cr {z_1} \hfill \cr} \right|;\left| \matrix{ {z_2} \hfill \cr {z_1} \hfill \cr} \right.\left. \matrix{ {x_2} \hfill \cr {x_1} \hfill \cr} \right|;\left| \matrix{ {x_2} \hfill \cr {x_1} \hfill \cr} \right.\left. \matrix{ {y_2} \hfill \cr {y_1} \hfill \cr} \right|} \right) \cr & = - \left[ {\overrightarrow b ,\overrightarrow a } \right]. \cr} \)
LG b
\(\eqalign{\left[ {\overrightarrow a ,\overrightarrow a } \right] = \overrightarrow 0\cr} \)
Lời giải chi tiết:
Từ câu a) ta có \(\left[ {\overrightarrow a ,\overrightarrow a } \right] = - \left[ {\overrightarrow a ,\overrightarrow a } \right]\) , suy ra \(\left[ {\overrightarrow a ,\overrightarrow a } \right] = \overrightarrow 0 \).
LG c
\(\eqalign{\left[ {k\overrightarrow a ,\overrightarrow b } \right] = k\left[ {\overrightarrow a ,\overrightarrow b } \right] = \left[ {\overrightarrow a ,k\overrightarrow b } \right] & \cr} \)
Lời giải chi tiết:
\(\eqalign{ & k\left[ {\overrightarrow a ,\overrightarrow b } \right] = \left( {k\left| \matrix{ {y_1} \hfill \cr {y_2} \hfill \cr} \right.\left. \matrix{ {z_1} \hfill \cr {z_2} \hfill \cr} \right|;k\left| \matrix{ {z_1} \hfill \cr {z_2} \hfill \cr} \right.\left. \matrix{ {x_1} \hfill \cr {x_2} \hfill \cr} \right|;k\left| \matrix{ {x_1} \hfill \cr {x_2} \hfill \cr} \right.\left. \matrix{ {y_1} \hfill \cr {y_2} \hfill \cr} \right|} \right) \cr & = \left( {\left| \matrix{ k{y_1} \hfill \cr {y_2} \hfill \cr} \right.\left. \matrix{ k{z_1} \hfill \cr {z_2} \hfill \cr} \right|;\left| \matrix{ k{z_1} \hfill \cr {z_2} \hfill \cr} \right.\left. \matrix{ k{x_1} \hfill \cr {x_2} \hfill \cr} \right|;\left| \matrix{ k{x_1} \hfill \cr {x_2} \hfill \cr} \right.\left. \matrix{ k{y_1} \hfill \cr {y_2} \hfill \cr} \right|} \right) \cr & = \left[ {k\overrightarrow a ,\overrightarrow b } \right]. \cr} \)
Tương tự \(k\left[ {\overrightarrow a ,\overrightarrow b } \right] = \left[ {\overrightarrow a ,k\overrightarrow b } \right].\)
LG d
\(\eqalign{\left[ {\overrightarrow c ,\overrightarrow a + \overrightarrow b } \right] = \left[ {\overrightarrow c ,\overrightarrow a } \right] + \left[ {\overrightarrow c ,\overrightarrow b } \right]\cr} \)
Lời giải chi tiết:
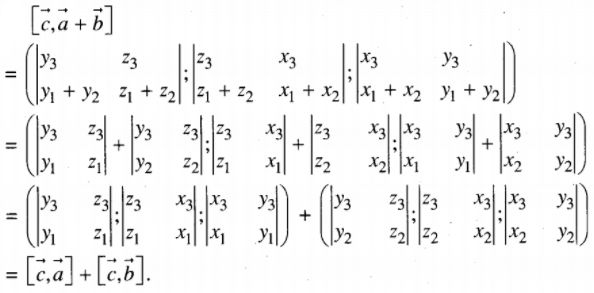
LG e
\(\eqalign{\overrightarrow a \left[ {\overrightarrow b ,\overrightarrow c } \right] = \left[ {\overrightarrow a ,\overrightarrow b } \right].\overrightarrow c \cr} \)
Lời giải chi tiết:
\(\eqalign{ & \overrightarrow a .\left[ {\overrightarrow b ,\overrightarrow c } \right] \cr&= {x_1}\left( {\left| \matrix{ {y_2} \hfill \cr {y_3} \hfill \cr} \right.\left. \matrix{ {z_2} \hfill \cr {z_3} \hfill \cr} \right| + {y_1}\left| \matrix{ {z_2} \hfill \cr {z_3} \hfill \cr} \right.\left. \matrix{ {x_2} \hfill \cr {x_3} \hfill \cr} \right| + {z_1}\left| \matrix{ {x_2} \hfill \cr {x_3} \hfill \cr} \right.\left. \matrix{ {y_2} \hfill \cr {y_3} \hfill \cr} \right|} \right) \cr & = {x_3}\left( {\left| \matrix{ {y_1} \hfill \cr {y_2} \hfill \cr} \right.\left. \matrix{ {z_1} \hfill \cr {z_2} \hfill \cr} \right| + {y_3}\left| \matrix{ {z_1} \hfill \cr {z_2} \hfill \cr} \right.\left. \matrix{ {x_1} \hfill \cr {x_2} \hfill \cr} \right| + {z_3}\left| \matrix{ {x_1} \hfill \cr {x_2} \hfill \cr} \right.\left. \matrix{ {y_1} \hfill \cr {y_2} \hfill \cr} \right|} \right) \cr & =\left[ {\overrightarrow a ,\overrightarrow b } \right].\overrightarrow c \cr} \)
LG g
\(\eqalign{\left| {{{\left[ {\overrightarrow a ,\overrightarrow b } \right]}^2}} \right| = {\left| {\overrightarrow a } \right|^2}.{\left| {\overrightarrow b } \right|^2} - {(\overrightarrow a .\overrightarrow b )^2}. \cr} \)
Lời giải chi tiết:
\(\eqalign{ VP &= {\left| {\overrightarrow a } \right|^2}.{\left| {\overrightarrow b } \right|^2} - {(\overrightarrow a .\overrightarrow b )^2} \cr&= {\left| {\overrightarrow a } \right|^2}.{\left| {\overrightarrow b } \right|^2} - {\left| {\overrightarrow a } \right|^2}.{\left| {\overrightarrow b } \right|^2}\cos^2 \alpha \cr & = {\left| {\overrightarrow a } \right|^2}.{\left| {\overrightarrow b } \right|^2}(1 - {\cos ^2}\alpha ) = {\left| {\overrightarrow a } \right|^2}.{\left| {\overrightarrow a } \right|^2}.{\sin ^2}\alpha \cr} \)
\( = {\left| {\left[ {\overrightarrow a ,\overrightarrow b } \right]} \right|^2} = VT\) ( ở đây \(\alpha = (\overrightarrow a ,\overrightarrow b ))\).
dapandethi.vn
