Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau :
LG a
\(y = {x^2} + x + 1;\)
Lời giải chi tiết:
Ta có thể viết hàm số \(y = {x^2} + x + 1\) dưới dạng
\(y = {\left( {x + {1 \over 2}} \right)^2} + {3 \over 4}\)
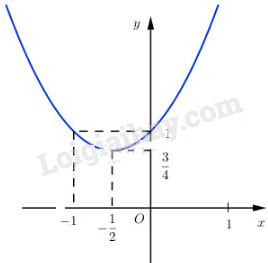
Từ đó suy ra đồ thị của nó là một parabol hướng bề lõm lên trên và có đỉnh tại \(\left( { - {1 \over 2};{3 \over 4}} \right)\) ; hàm số đã cho nghịch biến trên khoảng \(\left( { - \infty ; - {1 \over 2}} \right)\) , đồng biến trên khoảng \(\left( { - {1 \over 2}; + \infty } \right)\)
và có giá trị nhỏ nhất bằng \({3 \over 4}\) khi \(x = - {1 \over 2}.\)
Để vẽ đồ thị của hàm số này, ta lập bảng một vài giá trị của nó như sau
|
\(x\) |
-2 |
-1 |
\( - {1 \over 2}\) |
0 |
1 |
|
\(y\) |
3 |
1 |
\({3 \over 4}\) |
1 |
3 |
Đồ thị của hàm số có dạng như hình sau:
LG b
\(y = - 2{x^2} + x - 2;\)
Lời giải chi tiết:
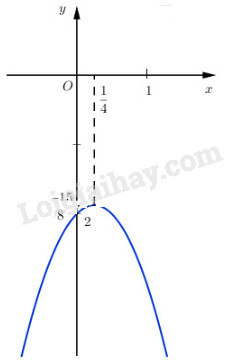
Đưa hàm số đã cho về dạng \(y = - 2{\left( {x - {1 \over 4}} \right)^2} - {{15} \over 8}.\)
Từ đó suy ra hàm số đồng biến trên khoảng \(\left( { - \infty ;{1 \over 4}} \right)\) , nghịch biến trên khoảng \(\left( {{1 \over 4}; + \infty } \right)\) và có giá trị lớn nhất bằng \( - {{15} \over 8}\) khi \(x = {1 \over 4}.\).
Đồ thị hàm số:
LG c
\(y = - {x^2} + 2x - 1;\)
Lời giải chi tiết:
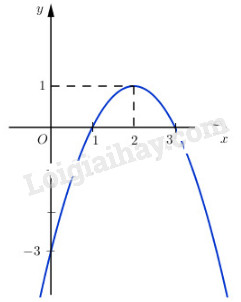
Hàm số \(y = - {x^2} + 2x - 1\) đồng biến trên khoảng \(\left( { - \infty ;2} \right)\); nghịch biến trên khoảng \(\left( {2; + \infty } \right)\).
Đồ thị hàm số:
LG d
\(y = {1 \over 2}{x^2} - x + 2.\)
Lời giải chi tiết:
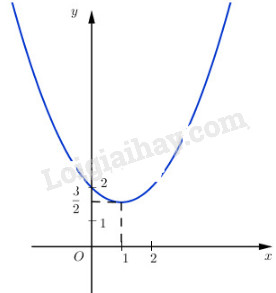
Hàm số \(y = {1 \over 2}{x^2} - x + 2.\) đồng biến trên khoảng \(\left( {1; + \infty } \right)\); nghịch biến trên khoảng \(\left( { - \infty ;1} \right)\)
Đồ thị hàm số:
dapandethi.vn
