Video hướng dẫn giải
Làm tính nhân:
LG a.
\(\eqalign{
& \,\,\left( {{1 \over 2}x + y} \right)\left( {{1 \over 2}x + y} \right) } \)
Phương pháp giải:
Áp dụng qui tắc nhân đa thức với đa thức để nhân phá ngoặc rồi rút gọn biểu thức.
Lời giải chi tiết:
\(\eqalign{
& \,\,\left( {{1 \over 2}x + y} \right)\left( {{1 \over 2}x + y} \right) \cr
& = {1 \over 2}x.\left( {{1 \over 2}x + y} \right) + y.\left( {{1 \over 2}x + y} \right) \cr
& = {1 \over 2}x.{1 \over 2}x + {1 \over 2}x.y + y.{1 \over 2}x + y.y \cr
& = {1 \over 4}{x^2} + {1 \over 2}xy + {1 \over 2}xy + {y^2} \cr
& = {1 \over 4}{x^2} + \left( {{1 \over 2}xy + {1 \over 2}xy} \right) + {y^2} \cr
& = {1 \over 4}{x^2} + xy + {y^2} \cr} \)
LG b.
\(\eqalign{
& \,\,\left( {x - {1 \over 2}y} \right)\left( {x - {1 \over 2}y} \right) \cr} \)
Phương pháp giải:
Áp dụng qui tắc nhân đa thức với đa thức để nhân phá ngoặc rồi rút gọn biểu thức.
Lời giải chi tiết:
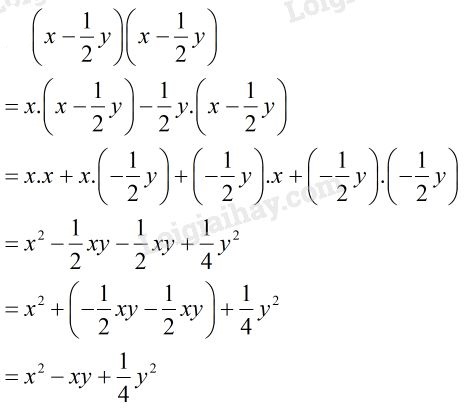
dapandethi.vn
