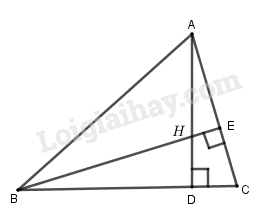
Cho tam giác có ba góc nhọn \(ABC\) (h.32). Hai đường cao \(AD\) và \(BE\) của tam giác cắt nhau tại \(H\).
Câu 15a
a) Trong hình \(32\), số tam giác vuông là:
A. \(2\) B. \(3\)
C. \(4\) D. \(6\)
Khoanh tròn vào chữ cái trước khẳng định đúng.
Phương pháp giải:
Phương pháp:
Tam giác vuông là tam giác có \(1\) góc vuông.
Lời giải chi tiết:
Cách giải:
Các tam giác vuông là: \(\Delta ADB,\Delta ADC,\Delta AEB,\) \(\Delta CEB,\Delta AEH,\Delta BDH\).
Vậy có \(6\) tam giác vuông.
Câu 15b
Số các tam giác cùng đồng dạng với nhau là:
A. \(2\) B. \(3\)
C. \(4\) D. \(5\)
E. \(6\)
Khoanh tròn vào chữ cái trước khẳng định đúng.
Phương pháp giải:
Phương pháp:
Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Lời giải chi tiết:
Cách giải:
Xét \(\Delta AEH\) và \(\Delta BDH\) có:
\(\widehat {AEH} = \widehat {BDH} = {90^0}\left( {gt} \right)\)
\(\widehat {AHE} = \widehat {BHD}\) (đối đỉnh)
\( \Rightarrow \Delta AEH \backsim \Delta BDH\left( {g.g} \right)\)
Xét \(\Delta AEH\) và \(\Delta ADC\) có:
\(\widehat {AEH} = \widehat {ADC} = {90^0}\left( {gt} \right)\)
Chung \(\widehat A\)
\( \Rightarrow \Delta AEH \backsim \Delta ADC\left( {g.g} \right)\)
Xét \(\Delta ADC\) và \(\Delta BEC\) có:
\(\widehat {ADC} = \widehat {BEC} = {90^0}\left( {gt} \right)\)
Chung \(\widehat C\)
\( \Rightarrow \Delta ADC \backsim \Delta BEC\left( {g.g} \right)\)
Vậy các tam giác cùng đồng dạng với nhau là: \(\Delta AEH\), \(\Delta BDH\), \(\Delta BEC\), \(\Delta ADC\).
Có \(4\) tam giác.
Chọn C.
Câu 15c
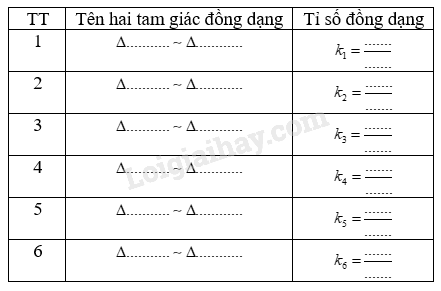
Hãy điền từng cặp tam giác đồng dạng (viết theo đúng thứ tự các đỉnh tương ứng) và tỉ số đồng dạng của chúng vào chỗ trống trong bảng dưới đây:
Phương pháp giải:
Phương pháp:
Sử dụng kết quả câu b và điền vào bảng.
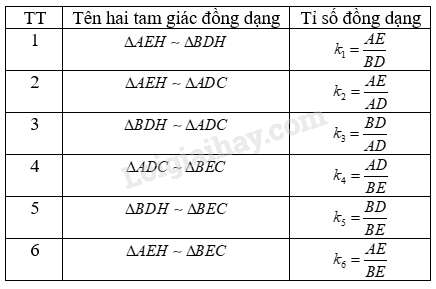
Lời giải chi tiết:
Cách giải:
dapandethi.vn
