Bài 29 trang 91 Vở bài tập toán 8 tập 2

Đề bài

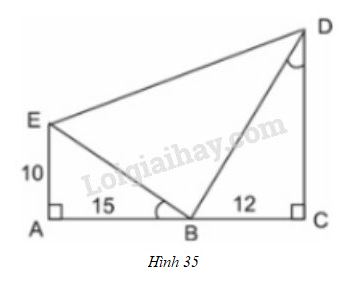
Hình 35 cho biết \(\widehat{EBA} = \widehat{BDC}\).

a) Trong hình vẽ, có bao nhiêu tam giác vuông? Hãy kể tên các tam giác đó.

b) Cho biết \(AE = 10cm, AB = 15cm, BC = 12cm\). Hãy tính độ dài các đoạn thẳng \(CD, BE, BD\) và \(ED\) (làm tròn đến chữ số thập phân thứ nhất).

c) So sánh diện tích tam giác \(BDE\) với tổng diện tích hai tam giác \(AEB\) và \(BCD\).

Lời giải chi tiết

Ta có: \(\widehat{EBA} = \widehat{BDC}\) (giả thiết) mà \(\widehat{BDC} + \widehat{CBD}={90^0}\) (do tam giác BCD vuông tại C)  

\( \Rightarrow \widehat{EBA} + \widehat{CBD}={90^0}\) 

Vậy \(\widehat{EBD} = {180^0} - (\widehat{EBA}+ \widehat{CBD})\)\(\, = {180^o} - {90^o} = {90^o}\)

Vậy trong hình vẽ có ba tam giác vuông đó là:

\(∆ABE, ∆CBD, ∆EBD.\)

b) \(∆ABE\) và \(∆CDB\) có:

\(\widehat{A} = \widehat{C}=90^o\)

\(\widehat{ABE}= \widehat{CDB}\) (giả thiết)

\( \Rightarrow  ∆ABE ∽ ∆CDB\) (g-g)

\( \Rightarrow \dfrac{AB}{CD} = \dfrac{AE}{CB}\) (tính chất hai tam giác đồng dạng)

\( \Rightarrow CD = \dfrac{AB.CB}{AE} = 18\, (cm)\)

- Áp dụng định lí pitago ta có:

\( ∆ABE\) vuông tại \(A\)

\( \Rightarrow  BE = \sqrt{AE^{2}+AB^{2}}\) \(\,=\sqrt{10^{2}+15^{2}}\) \( \approx  18\, (cm)\).

 \(∆BCD\) vuông tại \(C\)

\( \Rightarrow BD = \sqrt {B{C^2} + D{C^2}}  \) \(= \sqrt {{{12}^2} + {{18}^2}}  \approx 21,6\,\,cm\)

\(∆EBD\) vuông tại \(B\)

\( \Rightarrow  ED = \sqrt{EB^{2}+BD^{2}}\) \(=\sqrt{325+ 468} \approx 28,2\, (cm)\)

c) Ta có: 

\(S_{ABE} + S_{DBC}\)

\(= \dfrac{1}{2}AE.AB + \dfrac{1}{2}BC.CD\) 

\(= \dfrac{1}{2}. 10.15 + \dfrac{1}{2}.12.18\)

\(= 75 + 108 = 183\;cm^2\).

Ta có: \(A{\rm{E}}//DC\,\,\left(\text{ cùng } { \bot AC} \right) \Rightarrow \) \(ACDE\) là hình thang.

\(S_{ACDE} = \dfrac{1}{2}.(AE + CD).AC\)

\(= \dfrac{1}{2}.(10 + 18).27= 378\;cm^2\)

\( \Rightarrow S_{EBD} = S_{ACDE} - (S_{ABE}+ S_{DBC})\)\(\; = 378 - 183 = 195\,cm^2\)

\(S_{EBD}> S_{ABE} + S_{DBC}\) \(( 195 > 183)\).

dapandethi.vn