Đề bài
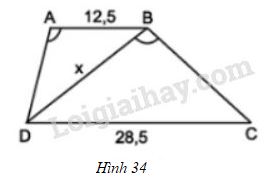
Tính độ dài \(x\) của đoạn thẳng \(BD\) trong hình 34 (Làm tròn đến chữ thập phân thứ nhất), biết rằng \(ABCD\) là hình thang (\(AB // CD\)); \(AB= 12,5cm; CD= 28,5cm\); \(\widehat{DAB} = \widehat{DBC}\).
Phương pháp giải - Xem chi tiết
Áp dụng:
- Định lí: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.
- Tính chất hai tam giác đồng dạng, tia phân giác.
Lời giải chi tiết
Xét \(ABD\) và \(BDC\)
Ta có: \(\widehat{DAB}\) = \(\widehat{DBC}\) (theo giả thiết)
\(\widehat{ABD}\) = \(\widehat{BDC}\) (hai góc so le trong)
Do đó \( ∆ABD ∽ ∆BDC\) (Trường hợp đồng dạng thứ ba).
Suy ra \(\dfrac{AB}{BD} = \dfrac{BD}{DC}\) \( \Leftrightarrow B{D^2} = AB.DC\)
hay \(x^2=12,5.28,5\) \( \Leftrightarrow x = \sqrt {12,5.28,5} \)
Tính trên máy tính bỏ túi (và làm tròn số) được \( x \approx 18,9 cm\).
dapandethi.vn
