Câu 4.
Hình thang \(ABCD\;(AB//CD)\) có \(\widehat D - \widehat A = {40^o}\). Số đo góc \(A\) bằng:
\(\eqalign{
& (A)\,\,{80^o}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(B)\,\,{70^o} \cr
& (C)\,\,{50^o}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(D)\,\,{110^o} \cr} \)
Phương pháp giải:
Sử dụng:
- Hình thang là tứ giác có hai cạnh đối song song.
- Một đường thẳng cắt hai đường thẳng song song tạo ra cặp góc trong cùng phía bù nhau.
Giải chi tiết:
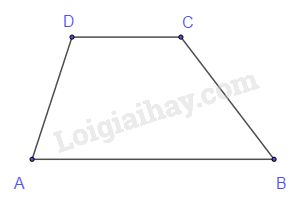
Vì \((AB//CD)\) nên \(\widehat A + \widehat D = {180^o}\) (1) (hai góc trong cùng phía).
\(\widehat D - \widehat A = {40^o} \Rightarrow \widehat D = \widehat A + {40^o}\;\;\;(2)\)
Thay (2) và (1) ta được:
\(\eqalign{
& \widehat A + \widehat A + {40^o} = {180^o} \cr
& 2\widehat A = {180^o} - {40^o} \cr
& \widehat A = {140^o}:2 = {70^o} \cr} \)
Chọn B.
Câu 5.
Một hình thang có hai góc bằng \(60^o\) và \(40^o\). Hai góc còn lại bằng
\(\eqalign{
& (A)\,\,{100^o}\,\,\text{và}\,\,{160^o} \cr
& (B)\,\,{140^o}\,\,\text{và}\,\,{120^o} \cr
& (C)\,\,{40^o}\,\,\text{và}\,\,{140^o} \cr
& (D)\,\,{120^o}\,\,\text{và}\,\,{60^o} \cr} \)
Phương pháp giải:
Sử dụng:
- Hình thang là tứ giác có hai cạnh đối song song.
- Một đường thẳng cắt hai đường thẳng song song tạo ra cặp góc trong cùng phía bù nhau.
Giải chi tiết:
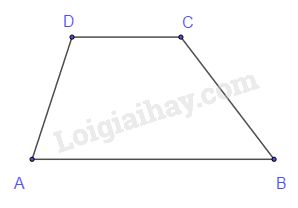
Giả sử hình thành \(ABCD\;(AB//CD)\) có \(\widehat A = {60^o},\,\widehat B = {40^o}\)
Vì \(AB//CD\) nên \(\widehat A + \widehat D = {180^o}\) (hai góc trong cùng phía).
\(\Rightarrow \widehat D = {180^o} - {60^o} = {120^o}\)
\(\widehat B + \widehat C = {180^o}\) (hai góc trong cùng phía).
\( \Rightarrow \widehat C = {180^o} - {40^o} = {140^o}\)
Chọn B.
Câu 6.
Hình thang vuông \(ABCD\) (đáy \(AB, CD\)) có \(\widehat A = {90^o},\,\widehat C = {65^o}\).
Hiệu \(\widehat B - \widehat D\) bằng
\(\eqalign{
& (A)\,\,{25^o}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(B)\,\,{35^o} \cr
& (C)\,\,{45^o}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(D)\,\,{15^o} \cr} \)
Phương pháp giải:
Sử dụng:
- Hình thang là tứ giác có hai cạnh đối song song.
- Một đường thẳng cắt hai đường thẳng song song tạo ra cặp góc trong cùng phía bù nhau.
Giải chi tiết:
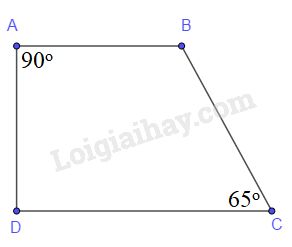
Vì \(AB//CD\) nên \(\widehat A + \widehat D = {180^o}\) (hai góc trong cùng phía)
\( \Rightarrow \widehat D = {180^o} - \widehat A = {180^o} - {90^o} = {90^o}\)
\(\widehat C + \widehat B = {180^o}\) (hai góc trong cùng phía)
\(\eqalign{
& \Rightarrow \widehat B = {180^o} - \widehat C = {180^o} - {65^o} = {115^o} \cr
& \Rightarrow \widehat B - \widehat D = {115^o} - {90^o} = {25^o} \cr} \)
Chọn A.
dapandethi.vn
