Đề bài
Hình thang \(ABCD\) (\(AB // CD\)) có \(\widehat{A}-\widehat{D}={20^0}\), \(\widehat{B}=2\widehat{C}\). Tính các góc của hình thang.
Phương pháp giải - Xem chi tiết
Áp dụng tính chất: Nếu một đường thẳng cắt hai đường thẳng song song thì tổng hai góc trong cùng phía bù nhau.
Lời giải chi tiết
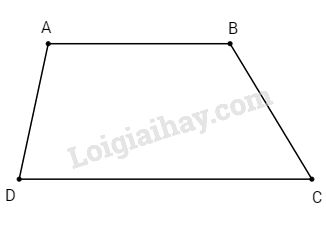
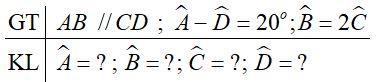
\(AB//CD\) nên \(\widehat A + \widehat D = {180^0}\) (hai góc trong cùng phía)
Ta lại có \(\widehat A - \widehat D = {20^0}\) nên \(\widehat D = \left( {{{180}^0} - {{20}^0}} \right):2 = {80^0}.\)
Suy ra \(\widehat{A}=20^0 + 80^0= 100^0\)
\(AB//CD\) nên \(\widehat{B}+\widehat{C}=180^0\). Ta lại có \(\widehat{B}=2\widehat{C}\)
nên \(3\widehat C = {180^0},\) suy ra \(\widehat C = {180^0}:3 = {60^0},\) \(\widehat{B}= 2.60^0 =120^0\)
Chú ý: \(\widehat{B}+\widehat{C}=180^0\) (vì hai góc trong cùng phía)
dapandethi.vn
