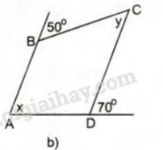
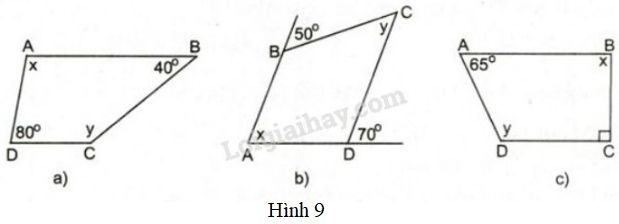
Tìm \(x\) và \(y\) trên hình \(9\), biết rằng \(ABCD\) là hình thang có đáy là \(AB\) và \(CD.\)
LG a
Phương pháp giải:
Áp dụng các tính chất của một đường thẳng cắt hai đường thẳng song song: hai góc trong cùng phía bù nhau, hai góc đồng vị bằng nhau, hai góc so le trong bằng nhau.
Giải chi tiết:
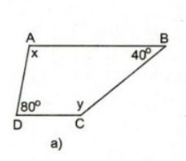
Ở hình 9a) ta có:
\(x = {180^0} - {80^0} = {100^0}\) (hai góc trong cùng phía, \(AB//DC\))
\( y = {180^0} - {40^0} = {140^0}\) (hai góc trong cùng phía, \(AB//DC\))
LG b
Phương pháp giải:
Áp dụng các tính chất của một đường thẳng cắt hai đường thẳng song song: hai góc trong cùng phía bù nhau, hai góc đồng vị bằng nhau, hai góc so le trong bằng nhau.
Giải chi tiết:
Ở hình 9b) ta có:
\( x ={70^0} \) (hai góc đồng vị, \(AB//DC\))
\(y ={50^0} \) (hai góc so le trong)
LG c
Phương pháp giải:
Áp dụng các tính chất của một đường thẳng cắt hai đường thẳng song song: hai góc trong cùng phía bù nhau, hai góc đồng vị bằng nhau, hai góc so le trong bằng nhau.
Giải chi tiết:
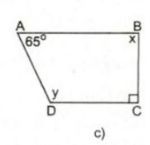
Ở hình 9c) ta có:
\( x = {180^0} - {90^0} = {90^0}\) (hai góc trong cùng phía, \(AB//DC\))
\(y = {180^0} - {65^0} = {115^0}\) (hai góc trong cùng phía, \(AB//DC\))
dapandethi.vn