Câu 4.
Khoanh tròn vào chữ cái trước câu trả lời đúng.
Một hình thoi có hai đường chéo bằng \(12\,cm\) và \(8\,cm\). Diện tích tứ giác có bốn đỉnh là trung điểm của bốn cạnh của hình thoi bằng
(A) \(48\,cm^2\) (B) \(24\,cm^2\)
(C) \(12\,cm^2\) (D) \(96\,cm^2\)
Phương pháp giải:
Phương pháp giải:
Công thức tính diện tích hình chữ nhật có hai cạnh kề nhau là \(a,b\) là \(S = a.b\).
Lời giải chi tiết:
Lời giải:
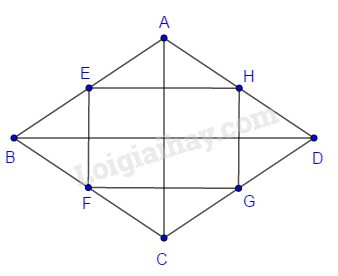
Hình thoi \(ABCD\) có \(AB=8;BD=12\)
\(E,F,G,H\) lần lượt là trung điểm của \(AB,BC,CD,DA.\)
Tam giác \(ABC\) có \(EA=EB;FB=FC\) nên \(EF\) là đường trung bình của \(\Delta ABC\)
\( \Rightarrow EF//AC;\,\,EF = \dfrac{1}{2}AC\)
Chứng minh tương tự:
\(\begin{gathered}
HG//AC;\,\,HG = \frac{1}{2}AC \hfill \\
EH//BD;\,\,EH = \frac{1}{2}BD \hfill \\
FG//BD;\,\,FG = \frac{1}{2}BD \hfill \\
\end{gathered} \)
\(\left. \begin{gathered}
EF//AC \hfill \\
EH//BD \hfill \\
AC \bot BD \hfill \\
\end{gathered} \right\} \Rightarrow EF \bot EH\)
Do đó tứ giác \(EFGH\) là hình chữ nhật.
\(\eqalign{
& {S_{EFGH}} = EF.EH = {1 \over 2}AC.{1 \over 2}BD \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\, \;\;\;= {1 \over 4}.AC.BD = {1 \over 4}.8.12 \cr& \,\,\,\,\,\,\,\,\,\,\,\,\,\, \;\;\;= 24\,\,\left( {c{m^2}} \right) \cr} \)
Chọn B.
Câu 5.
Một hình chữ nhật có chiều dài \(12m\), chiều rộng \(8m\). Một hình vuông có chu vi bằng chu vi hình chữ nhật. Diện tích của hình vuông đó bằng
(A) \(100\,m^2\) (B) \(40\,m^2\)
(C) \(25\,m^2\) (D) \(1600\,m^2\)
Phương pháp giải:
Phương pháp giải:
Sử dụng:
- Công thức tính chu vi hình chữ nhật là \(2(a+b)\)
\(a,b\) lần lượt là chiều dài và chiều rộng của hình chữ nhật.
- Công thức tính chu vi hình vuông có cạnh \(a\) là \(4a\)
- Công thức tính diện tích hình vuông có cạnh \(a\) là \(a^2\).
Lời giải chi tiết:
Lời giải:
Chu vi hình chữ nhật là:
\(2.\left( {12 + 8} \right) = 40\,\,\left( m \right)\)
Giả sử cạnh của hình vuông có cùng chu vi hình chữ nhật là \(a\;(m)\).
Ta có: \(4a = 40\, \Rightarrow a = 40:4 = 10\,\,\left( m \right)\)
Diện tích hình vuông là: \(10.10 = 100\,\,\left( {{m^2}} \right)\)
Chọn A.
Câu 6.
Khi mỗi cạnh của một hình vuông tăng thêm \(50\%\) thì diện tích hình vuông đó tăng thêm
(A) \(50\%\) (B) \(100\%\)
(C) \(225\%\) (D) \(125\%\)
Phương pháp giải:
Phương pháp giải:
Sử dụng: Diện tích hình vuông có cạnh \(a\) là \(a^2\).
Lời giải chi tiết:
Lời giải:
Gọi cạnh hình vuông ban đầu là \(a\) \((a>0)\).
Sau khi tăng \(50%\) thì cạnh của hình vuông là \(1,5a\).
Diên tích hình vuông sau khi tăng cạnh thêm \(50\%\) là:
\({\left( {1,5a} \right)^2} = 2,25{a^2}\)
Vậy diện tích hình vuông đó tăng thêm \(2,25{a^2} - {a^2} = 1,25{a^2} = 125\% .{a^2}\)
Chọn D.
dapandethi.vn
