Đề bài
Bài 1. Cho tam giác ABC nhọn, trung tuyến AD. Kẻ DN song song với AB \(\left( {N \in AC} \right)\). Kẻ DM song song với AC \(\left( {M \in AB} \right).\) MN cắt AD tại O.
a) Chứng minh A và D đối xứng với nhau qua điểm O.
b) Tính độ dài MN khi BC = 16 cm.
Bài 2. Cho hình thoi ABCD tân O. Trên tia đối của các tia BA, CB, DC, AD lần lượt lấy các điểm E, F, G, H sao cho BE = CF = DG = AH.
a) Chứng minh tứ giác EFGH là hình bình hành.
b) Chứng minh điểm O là tâm đối xứng của hình bình hành EFGH.
c) Hình thoi ABCD phải có điều kiện gì để EFGH trở thành hình thoi?
LG bài 1
Phương pháp giải:
Sử dụng:
Tứ giác có hai cặp cạnh đối song song là hình bình hành
Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy
Lời giải chi tiết:
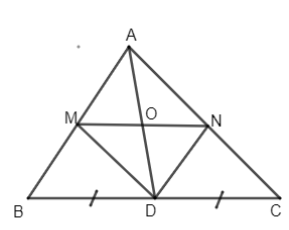
a) Ta có \(DN\parallel AB,DM\parallel AC\)
\( \Rightarrow ANDM\) là hình bình hành
\( \Rightarrow OA = OD\) hay A và D đối xứng với nhau qua điểm O.
b) D là trung điểm của BC (gt), \(DM\parallel AC\)
\( \Rightarrow M\) là trung điểm của AB
Tương tự N là trung điểm của AC
Do đó MN là đường trung bình của \(\Delta ABC\)
\( \Rightarrow MN = {1 \over 2}BC = {1 \over 2}.16 = 8cm\) .
LG bài 2
Phương pháp giải:
Sử dụng:
Tứ giác có hai cặp cạnh đối bằng nhau là hình bình hành
Điểm M đối xứng với N qua O nếu O là trung điểm của MN
Hình bình hành có hai cạnh kề bằng nhau là hình thoi
Hình thoi có một góc vuông là hình vuông.
Lời giải chi tiết:
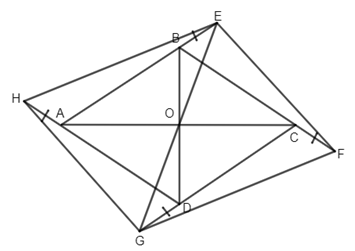
a) Ta có AB = CD (cạnh hình thoi)
BE = DC (gt)
\( \Rightarrow AB + BE = CD + DG\) hay AE = CG
Xét \(\Delta AHE\) và \(\Delta CFG\;(c.g.c)\) \(\Rightarrow HE = FG\)
Chứng minh tương tự ta có HG = FG
Do đó tứ giác EFGH là hình bình hành (các cạnh đối bằng nhau).
b) Nối E và G. Xét \(\Delta OBE\) và \(\Delta ODG\) có BE = DG (gt), \(\widehat {OBE} = \widehat {ODG}\) (so le trong), OB = OD (tính chất đường chéo của hình thoi ABCD)
\( \Rightarrow \Delta OBE = \Delta ODG\left( {c.g.c} \right)\)
\(\Rightarrow \widehat {BOE} = \widehat {DOG}\)
Mà \(\widehat {DOG} + \widehat {GOB} = {180^ \circ }\) (B, O , D thẳng hàng)
\( \Rightarrow \widehat {DOG} + \widehat {GOB} = {180^ \circ } \Rightarrow \) Ba điểm G, O, E thẳng hàng.
Chứng minh tương tự ta có H, O, F thẳng hàng.
Vậy O là tâm đối xứng của hình bình hành EFGH.
c) Hình bình hành EFGH là hình thoi \( \Leftrightarrow HE = {\rm{EF}}\)
\( \Leftrightarrow \Delta HAE = \Delta EBF\left( {c.c.c} \right)\)
\(\Leftrightarrow \widehat {HAE} = \widehat {EBF}\) mà \(\widehat {EBF} = \widehat {EAD}\) (đồng vị)
\( \Leftrightarrow \widehat {HAE} = \widehat {EAD}\) mà \(\widehat {HAE} + \widehat {EAD} = {180^ \circ }\) (kề bù)
\( \Leftrightarrow \widehat {HAE} = \widehat {EAD} = {90^ \circ } \Leftrightarrow \) hình thoi ABCD có 1 góc vuông.
\( \Leftrightarrow ABCD\) là hình vuông.
Vậy hình thoi ABCD phải là hình vuông thì hình bình hành EFGH trở thành hình thoi.
dapandethi.vn
