Đề bài
Bài 1. Cho hình thoi ABCD. Gọi O là giao điểm của hai đường chéo AC và BD. Đường thẳng qua O không song song với AD cắt AB tại M và CD tại N.
a) Chứng minh \(\Delta AOM = \Delta CON\).
b) Chứng tỏ tứ giác AMCN là hình bình hành.
Bài 2. Cho tam giác ABC vuông tại A có đường trung tuyến AM. Gọi D là trung điểm của AB, E là điểm đối xứng với M qua D.
a) Chứng minh tứ giác AEBM là hình thoi.
b) Gọi I là trung điểm AM. Chứng minh E, I, C thẳng hàng.
c) \(\Delta ABC\) có thêm điều kiện gì thì AEBM là hình vuông.
LG bài 1
Phương pháp giải:
Sử dụng:
Tính chất hai tam giác bằng nhau
Tứ giác có hai cặp cạnh đối bằng nhau là hình bình hành
Lời giải chi tiết:
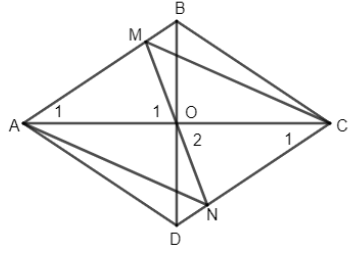
a) Ta có \(\widehat {{A_1}} = \widehat {{C_1}}\) (so le trong)
AO = CO (tính chất đường chéo hình thoi)
\(\widehat {{O_1}} = \widehat {{O_2}}\)
Vậy \(\Delta AOM = \Delta CON\left( {g.c.g} \right)\)
suy ra \( OM = ON.\)
b) Xét tứ giác AMCN có OM = ON (cmt), OA = OC (gt)
Do đó AMCN là hình bình hành.
LG bài 2
Phương pháp giải:
Sử dụng:
Tứ giác có hai cặp cạnh đối bằng nhau là hình bình hành
Hình bình hành có hai cạnh kề bằng nhau là hình thoi
Hình thoi có hai đường chéo bằng nhau là hình vuông
Lời giải chi tiết:
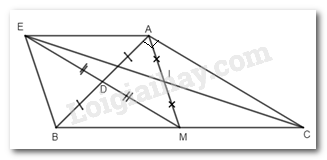
a) Ta có DA = DB, DE = DM (tính chất đối xứng)
\( \Rightarrow AEBM\) là hình bình hành.
Lại có MA = BM (trung tuyến tam giác vuông bằng nửa cạnh huyển).
Vậy AEBM là hình thoi.
b) Ta có \(AE//BM\) và AE = BM (vì AEBM là hình thoi) mà MC = BM
\( \Rightarrow AE//MC\) và \(AE = MC.\)
Do đó tứ giác AEMC là hình bình hành, I là trung điểm của đường chéo AM nên đường chéo thứ hai EC phải qua I hay ba điểm E, I, C thằng hàng.
c) Hình thoi AEBM là hình vuông \( \Leftrightarrow AB = EM\) hay EM = AC
\( \Leftrightarrow AB = AC \Leftrightarrow \Delta ABC\) vuông cân
dapandethi.vn
