Đề bài
Trên các cạnh BC và CD của hình vuông ABCD lấy các điểm E và F sao cho
\(\widehat {EAF} = 45^\circ \) . Các đoạn thẳng AE, AF cắt BD theo thứ tự ở H và K. Chứng minh tứ giác EHKF nội tiếp.
Phương pháp giải - Xem chi tiết
Tứ giác có 2 góc bằng nhau cùng nhìn 1 cạnh thì nội tiếp được. Ta chứng minh góc FKE bằng góc FHE bằng 90 độ cùng nhìn cạnh EF.
Lời giải chi tiết
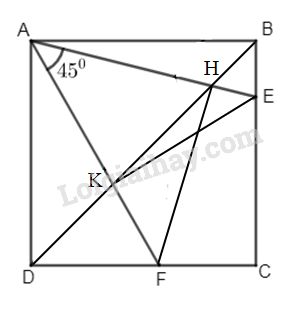
Ta có tứ giác ADFH có \(\widehat {EAF} = \widehat {BDC} = 45^\circ \)
Mà 2 góc này cùng nhìn cạnh HF. Nên tứ giác ADFH nội tiếp
\( \Rightarrow \widehat {ADF} + \widehat {AHF} = 180^\circ \) mà \(\widehat {ADF} = 90^\circ \)
\(\Rightarrow \widehat {AHF} = 90^\circ \Rightarrow \widehat {FHE} = 90^\circ .\)
Chứng minh tương tự ta có \(\widehat {FKE} = 90^\circ \).
Suy ra tứ giác EHKF có góc FHE = góc FKE và cùng nhìn cạnh EF
Do đó EHKF là tứ giác nội tiếp.
dapandethi.vn
