Đề bài
Cho hai đường tròn (O) và (O’) bằng nhau và cắt nhau tại hai điểm phân biệt A và B. Kẻ các đường kính AOC và AO’D. Hãy so sánh các cung: \(\overparen{ BC}\) và \(\overparen{BD}\) của (O) và (O’).
Phương pháp giải - Xem chi tiết
Sử dụng:
Tam giác có 1 cạnh là đường kính là tam giác vuông
Hai dây bằng nhau của hai đường tròn bằng nhau chắn các cung bằng nhau
2 Góc nội tiếp bằng nhau chắn hai cung bằng nhau
Lời giải chi tiết
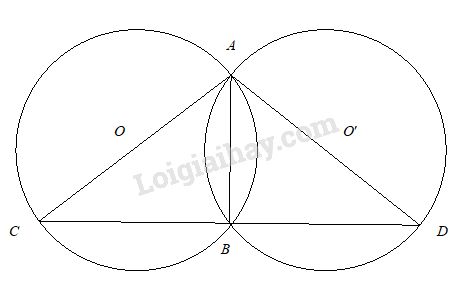
AC, AD lần lượt là đường kính của đường tròn (O) và (O’) nên \(AC = AD.\)
Xét các tam giác vuông ABC và ABD có:
+) \(AB\) chung,
+) \(AC = AD\)
Do đó \(∆ABC = ∆ABD\) ( cạnh huyền – cạnh góc vuông)
\(\Rightarrow BC = BD\)
\( \Rightarrow \overparen{ BC }= \overparen{ BD }\) và \(\overparen{ CAB} =\overparen{ DAB}\).
dapandethi.vn
