Đề bài
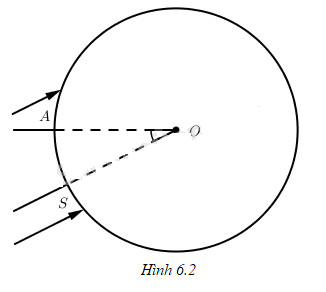
Ơ-ra-tơ-xten (Eratosthene), ở thế kỉ II trước Công nguyên (Nguyên giám đốc thư viện nổi tiếng ở A-lếch-xăng-đri (Alexandrie)) đã tìm cách tính bán kính của Trái Đất bằng cách đo khoảng cách giữa hai thành phố A-lếch-xăng-đri và Xy-en (Syene) là 8004km (theo đơn vị ngày nay; thuở đó các đoàn lạc đà đi từ thành phố này đến thành phố kia mất 50 ngày đường). Biết rằng, khi ở Xy-en tia sáng mặt trời chiếu thẳng đứng (nhìn thẳng xuống giếng sâu), thì ở A-lếch-xăng-đri, tia sáng mặt trời làm một góc \({\left( {7,1} \right)^0}\) với phương thẳng đứng. Hỏi làm sao Ơ-ra-tơ-xten suy ra được bán kính của Trái Đất (xấp xỉ 6400 km). (h.6.2)?
Lời giải chi tiết
Các tia sáng mặt trời chiếu song song xuống mặt đất: ở Xy-en (kí hiệu là \(S\)) chiếu thẳng góc với mặt đất, ở A-lếch-xăng-đri (kí hiệu là \(A\)) tạo với phương thẳng đứng một góc \({\left( {7,1} \right)^0}\) nên số đo cung trong \(AS\) là \({\left( {7,1} \right)^0}\). Gọi \(R\) (km) là bán kính của Trái Đất, thì do độ dài cung tròn \(AS\) bằng 800km, suy ra được
\(R = \dfrac{{800}}{{\dfrac{\pi }{{180}} \times 7,1}} = \dfrac{{800.180}}{{\pi \times 7,1}} \approx 6456\left( {km} \right)\).
dapandethi.vn
