Chọn đáp án đúng:
6.24
Cho cotα = -2/3 với π < α < π. Giá trị cosα là
A. \( - \dfrac{2}{{\sqrt {13} }}\)
B. \(\dfrac{2}{{\sqrt {13} }}\)
C. \(\dfrac{2}{5}\)
D. \( - \dfrac{{\sqrt {13} }}{2}\)
Lời giải chi tiết:
Cách 1.
1/( sin2 α) = 1 + cot2 α = 1 + 4/9 = 13/9 ⇒ sin2 α = 9/13.
Suy ra sinα = ±3/√13.
Vì π/2 < α < π nên sinα > 0. Vậy sinα = 3/√13.
Từ đó cosα = sinα.cotα = (-2)/√13.
Đáp án là A.
Cách 2.
cotα = (-2)/3 ⇒ tanα = (-3)/2;
1/( cos2 α) = 1 + tan2 α = 1 + 9/4 = 13/4 ⇒ cos2 α = 4/13.
Suy ra cosα = ±2/√13. Vì π/2 < α < π nên cosα < 0.
Vậy cosα = (-2)/√13 và đáp án là A.
Đáp án: A
6.25
Cho tanα = -√2/3. Giá trị của biểu thức \(M = \dfrac{{3\cos \alpha - 5\sin \alpha }}{{ - 2\cos \alpha + 3\sin \alpha }}\) là
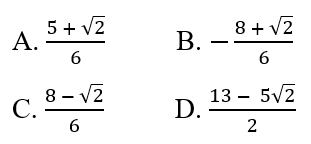
Lời giải chi tiết:
Cách 1. Suy luận
Vì tanα < 0 nên cosα và sinα trái dấu.
Nếu cosα > 0, sinα < 0 thì tử số của M dương, còn mẫu số âm, nên M < 0. Còn nếu cosα < 0, sinα > 0 thì tử số của M âm, mẫu số của M dương nên ta cũng có M < 0.
Do đó các phương án A, C, D bị loại và đáp án là B.
Cách 2. Tính trực tiếp.
Chia cả tử và mẫu của M sao cho cosα, ta được:
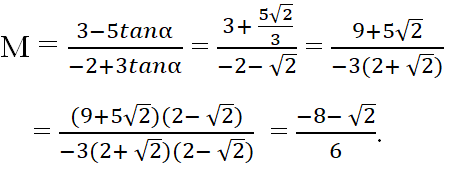
Đáp án: B
6.26
Cho cosα = √2/3 (0 <α < π/2 ). Giá trị của cot(α + 3π/2) là

Lời giải chi tiết:
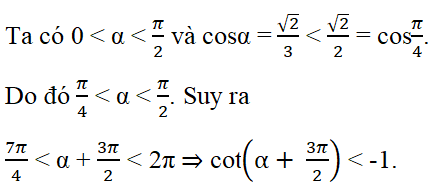
Vậy các phương án B, C, D bị loại và đáp án là A.
Đáp án: A
Cách khác:
Ta có: \(\cos \alpha = \dfrac{{\sqrt 2 }}{3}\) \( \Rightarrow {\sin ^2}\alpha = 1 - {\cos ^2}\alpha \) \( = 1 - \dfrac{2}{9} = \dfrac{7}{9}\)
\( \Rightarrow \sin \alpha = \pm \dfrac{{\sqrt 7 }}{3}\)
Vì \(0 < \alpha < \dfrac{\pi }{2}\) nên \(\sin \alpha > 0\), do đó \(\sin \alpha = \dfrac{{\sqrt 7 }}{3}\)
\( \Rightarrow \tan \alpha = \dfrac{{\sin \alpha }}{{\cos \alpha }}\) \( = \dfrac{{\sqrt 7 }}{3}:\dfrac{{\sqrt 2 }}{3} = \dfrac{{\sqrt {14} }}{2}\)
Mà \(\cot \left( {\alpha + \dfrac{{3\pi }}{2}} \right)\)\( = \cot \left( {2\pi - \dfrac{\pi }{2} + \alpha } \right)\) \( = \cot \left( { - \dfrac{\pi }{2} + \alpha } \right)\)
\( = \cot \left[ { - \left( {\dfrac{\pi }{2} - \alpha } \right)} \right]\) \( = - \cot \left( {\dfrac{\pi }{2} - \alpha } \right)\) \( = - \tan \alpha = - \dfrac{{\sqrt {14} }}{2}\)
Vậy \(\cot \left( {\alpha + \dfrac{{3\pi }}{2}} \right) = - \dfrac{{\sqrt {14} }}{2}\).
6.27
Cho tanα + cotα = -2. Giá trị của biểu thức N = tan3α + cot3α là
A. 3 B. 4
C. -2 D. 2
Lời giải chi tiết:
Cách 1.
Ta có:
\(\begin{array}{l}{\left( {\tan \alpha + \cot \alpha } \right)^2}\\ = {\tan ^2}\alpha + {\cot ^2}\alpha + 2\tan \alpha \cot \alpha \\ = \left( {{{\tan }^2}\alpha + {{\cot }^2}\alpha } \right) + 2\\ \ge 2\tan \alpha \cot \alpha + 2 = 2.1 + 2 = 4\\ \Rightarrow {\left( {\tan \alpha + \cot \alpha } \right)^2} \ge 4\\ \Rightarrow \left[ \begin{array}{l}\tan \alpha + \cot \alpha \ge 2\\\tan \alpha + \cot \alpha \le - 2\end{array} \right.\end{array}\)
Do đó tanα + cotα ≤ -2 hoặc tanα + cotα ≥ 2.
Dấu “=” xảy ra khi tanα = cotα = -1 hoặc tanα = cotα = 1.
Với giả thiết tanα + cotα = -2 thì tanα = cotα = -1.
Do đó tan3 α + cot3 α = -2
Đáp án là C.
Cách 2.
Áp dụng công thức
tan3 α + cot3 α = (tanα + cotα)( tan2 α – tanα.cotα + cot2 α)
= -2( tan2 α + cot2 α – 1)
Mà tan2 α + cot2 α = (tanα + cotα)2 - 2 tanα.cotα = 4 – 2 = 2.
Vậy tan3 α + cot3 α = -2(2-1) = -2.
Đáp án: C
6.28
Cho sinα = √5/4. Giá trị cos(α + π/2) là
A. \( - \dfrac{{4\sqrt 5 }}{5}\) B. \(\dfrac{{\sqrt 5 }}{4}\)
C. \(\dfrac{{\sqrt 3 }}{4}\) D. \( - \dfrac{{\sqrt 5 }}{4}\)
Lời giải chi tiết:
Cách 1
Ta có sinα > 0 nên
k2π < α < π + k2π, k ∈ Z ⇒ π/2 + k2π < α + π/2 < 3π/2 + k2π.
Do đó cos(α+ π/2) < 0, nên các phương án B, C bị loại. Mặt khác cos(α+ π/2) > -1 nên phương án A bị loại. Vậy đáp án là D.
Cách 2. Ta có
cos(α+ π/2) = cos(α- π/2+ π) = - cos(α- π/2) = - cos(π/2- α) = - sin α = -√5/4
Đáp án: D
6.29
Cho sinα = √6/3. Giá trị của biểu thức
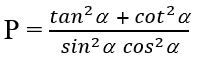
A. 51/7 B. 31/4
C. 45/4 D. 22/3
Lời giải chi tiết:
Cách 1. Suy luận.
Do \(\sin \alpha = \dfrac{{\sqrt 6 }}{3} \Rightarrow {\sin ^2}\alpha = \dfrac{2}{3}\) \( \Rightarrow {\cos ^2}\alpha = 1 - {\sin ^2}\alpha \) \( = 1 - \dfrac{2}{3} = \dfrac{1}{3}\)
Tử số của P lớn hơn hoặc bằng 2.
Mẫu số là sin2 a. cos2 a = 2/3. 1/3 = 2/9 < 1/4, nên P ≤ 8.
Do đó các phương án A, B, D bị loại. Đáp án là C.
Cách 2. Tính trực tiếp.
sina = √6/3 ⇒ sin2 a = 2/3 ⇒ cos2 a = 1/3.
Vậy tan2 a = 2, cot2 a = 1/2.
Do đó P = 45/4. Đáp án là C.
Đáp án: C
dapandethi.vn
