Đề bài
Cho tam giác ABC có điểm D nằm giữa B và C.
Chứng minh:
\({{AB + AC - BC} \over 2} < AD < {{AB + AC + BC} \over 2}\)
Lời giải chi tiết
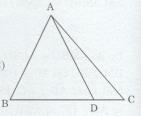
∆ABD có AB – BD < AD < AB + BD (bất đẳng thức trong tam giác)
∆ADC có AC – DC < AD < AC + DC (bất đẳng thức trong tam giác)
Do đó
\(AB –BD + AC –DC < AD + AD < AB + BD + AC + DC\)
\(=> AB + AC –BD – DC < 2AD < AB + AC + BD + DC\)
\(=> AB + AC – (BD + DC) < 2AD <AB + AC + (BD + DC)\)
=> AB + AC – BC < 2AD < AB + AC + BC
Vậy \({{AB + AC - BC} \over 2} < AD < {{AB + AC + BC} \over 2}\)
dapandethi.vn
