Đề bài
Cho tam giác ABC có E vả F lần lượt là trung điểm của AB và AC. Cho biết BF = 12 cm, CE = 9 cm và BC = 10 cm. Tính diện tích tam giác ABC.
Lời giải chi tiết
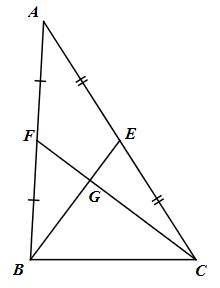
Gọi G là giao điểm của BF và CE. Theo bài 8, ta có \({S_{GBC}} = {1 \over 3}{S_{ABC}}\)
Mặt khác tam giác ABC có BF, CE là hai đường trung tuyến cắt nhau tại G.
\( \Rightarrow G\) là trọng tâm của tam giác ABC.
\( \Rightarrow GB = {2 \over 3}BF = {2 \over 3}.12 = 8\,\,\left( {cm} \right)\)
Và \(GC = {2 \over 3}CE = {2 \over 3}.9 = 6\,\,\left( {cm} \right)\)
Tam giác GBC có : \(G{B^2} + G{C^2} = B{C^2}\,\,\left( {{8^2} + {6^2} = {{10}^2}} \right)\)
\( \Rightarrow \Delta GBC\) vuông tại G (Định lí Pytago đảo)
Do đó \({S_{GBC}} = {1 \over 2}GB.GC = {1 \over 2}.8.6 = 24\,\,\left( {c{m^2}} \right)\)
Ta có \({S_{GBC}} = {1 \over 3}{S_{ABC}}\)
Vậy \({S_{ABC}} = 3{S_{GBC}} = 3.24 = 72\,\,\left( {c{m^2}} \right)\)
dapandethi.vn
